.
Abstract: the Suppes-Sen dominance relation is a weak and widely accepted criterion of distributive justice. We propose its application to Nash bargaining theory. The Nash Bargaining Solution (NBS) is characterised by replacing the controversial Independence of Irrelevant Alternatives axiom with an axiom embodying the Suppes-Sen principle. More precisely, maximality in the Suppes-Sen relation is shown to be equivalent to the NBS in the presence of Scale Covariance. The characterisation is far more robust than the standard one with respect to variations in the domain of bargaining problems. It is also shown that a subset of Nash's axioms imply the Suppes-Sen relation.
JEL class. number: C71, C78.
I am deeply indebted, with the usual disclaimers, to Paul Madden for comments, bibliographical suggestions, encouragement, and not least for originating my interest in the Suppes-Sen relation. Useful suggestions have also come from Vincenzo Denicolò, Joseph Greenberg, Paola Manzini, Herve Moulin and Fioravante Patrone.
In the axiomatic theory of bargaining initiated by Nash (1950) one defines a set of admissible bargaining problems (e.g., convex problems) and imposes some desirable requirements (axioms) on the solution function, which picks an element from each problem; the aim is to characterise uniquely such a function. One interpretation of the axioms is as properties that should be satisfied by the choices of a fair arbitrator (e.g., Myerson (1990, p. 372-3), Young (1994, ch. 7), Mas Colell et. al. (1995, ch. 22.E) and, implicitly, Hammond (1991), p. 203). The axioms that characterise the Nash Bargaining Solution (NBS) include the powerful Independence of Irrelevant Alternative (IIA), which has been extensively discussed and criticised. Indeed, although IIA and its variations may be viewed as a relevant criterion of rationality for individual choice, it is difficult to see it as a compelling requirement of fair arbitration. As Binmore (1992, p.196) puts it:
"Some authors misunderstand Nash's motives in formulating his bargaining solution and imagine that his axioms can be sensibly interpreted as criteria for a 'fair arbitration scheme' ... other axiom systems have been introduced to characterise other so-called 'bargaining solutions' that do make sense as fair arbitration schemes".
We think that Binmore's statement concerning Nash's axioms is correct. In this paper we aim to show that -whatever Nash's motives were- there are nonetheless very strong reasons to interpret Nash's solution as an expression of fairness. We will illustrate a striking property of the NBS, which supports this interpretation and allows a characterisation that dispenses with IIA altogether. It turns out that the NBS is the only scale covariant bargaining solution satisfying the weak and widely accepted criterion of distributive justice known as Suppes-Sen dominance (Suppes (1966), Sen (1970), chs. 9 and 9*),.
Given utility vectors x and y, x is said to Suppes-Sen dominate (SS-dominate) y if and only if there exists a permutation of x that Pareto dominates y. We refer to the application of this dominance criterion as the Suppes-Sen principle. To see how weak the principle is, just note that, mathematically, SS-dominance coincides with first-order stochastic dominance. When applied to social welfare functionals, it does not discriminate almost at all; it is, rather, a 'common denominator'. We quote from Sen (1970, p. 151):
"The conflicting claims of the maximin criterion and utilitarianism are difficult to resolve. Each has some attractive features and some unattractive ones. The [Suppes-Sen principle], when suitably constrained, seems to catch the most appealing common elements of the two. ... While it does not yield a complete social ordering, it does squeeze out as much juice as possible out of the use of "dominance" (or vector inequality), which is the common element in the maximin criterion, utilitarianism, and a number of other collective choice procedures involving interpersonal comparability".
There are two main ideas behind the Suppes-Sen principle. First, 'fair' decisions should be, in some sense, impersonal: if x is considered 'more just' than y, this judgement should not depend on the position of any particular prespecified individual. In this respect, the principle appears to be a combination of Pareto optimality with Anonymity. Secondly, ordinal interpersonal comparisons of utility are meaningful (recall how, in social choice theory, Arrow's (1951) impossibility theorem and in particular Sen's (1970, p. 123-30) analogous result when cardinal intensities of preferences are available imply that utilities must satisfy some form of interpersonal comparability if reasonable and defined social choices are to be made). As far as we are aware, the relevance of the Suppes-Sen principle to Nash bargaining theory viewed as a theory of fair arbitration has not been studied. We propose to do so, as follows.
In Nash's bargaining theory a disagreement point is given, which is relevant for the outcome of the problem. On our interpretation, a bargaining problem is a special but important kind of social decision problem. A fair arbitrator who accepts ordinal interpersonal utility comparisons will want to apply the Suppes-Sen principle to the players' utilities net of the disagreement utility. It should be obvious from our earlier remarks about social welfare functions that even in bargaining theory one cannot travel very far on the basis of SS-dominance alone, when the class of scale-dependent solutions is considered. For example, both the Utilitarian (Myerson (1981)) and the Egalitarian (Kalai (1977)) bargaining solutions will yield SS-undominated outcomes for each problem. At first blush, it might appear that also all scale covariant solutions which satisfy the axioms of Pareto optimality and Anonymity (or Symmetry) will be bound to be compatible with the Suppes-Sen principle; one particularly obvious candidate being the Kalai and Smorodinsky solution (KSS), identified with relative egalitarianism. Surprisingly, this is not the case. Even more surprisingly, there exists only one scale-covariant solution which yields SS-undominated outcomes in each bargaining problem, and this is the NBS (Theorem 3.2).
The validity of the last assertion as a mere mathematical fact is not in doubt, but one important point of interpretation should be discussed. Scale covariant bargaining solutions are able to determine solution outcomes without the use of interpersonal utility comparisons of any sort. What is the meaning, then, of adopting a criterion that hinges on such interpersonal comparisons, albeit of an ordinal nature? Our methodological premise is that it is logically meaningful to compare utilities across individuals, but that it is practically difficult, if not impossible, to obtain empirically the necessary scheme of interpersonal scaling. We quote from Elster and Roemer (1991, p. 10-11):
"Let us assume that there is a fact of the matter in an interpersonal comparison of well-being ... It does not follow that we could ever discover it. Statements about the past pose similar problems. We tend to assume that there is a fact of the matter by virtue of which statements about the past are true if true, false if false. We may never be able to establish what the fact of the matter is -for example, whether it was raining when Caesar crossed the Rubicon. But that does not affect the existence of a fact of the matter. In one sense, other minds are just as inaccessible to us as the past. We need not entairtain doubts about their existence and their essential similarity to our own, but we may despair at ever getting the details right".
In other words, suppose that an arbitrator knew that the increase in utility that Mr. A derives when moving from a situation when he cannot play the trumpet to one where he can is twice as much as the increase in utility that Mr. B derives when moving from a situation when he cannot play the drums to one where he can. Then, the arbitrator should use this information to adjudicate how much each is allowed to play (and disturb the other). In practice, the arbitrator will not receive such detailed information, and will be forced to decide by avoiding interpersonal utility comparisons. However, if he believes in the Suppes-Sen principle of justice, he will wish to decide in such a way that, if given the extra information, he would not be found in violation of the principle. In this sense is the NBS the only means to reconcile the two desiderata.
Beside yielding a novel characterisation of the NBS which dispenses with one of the controversial axioms in Nash's system, our approach has the added benefit of being robust, in various senses. First, it is robust to the choice of domain of the solution function. Nash (1950) confined himself to the class of convex problems; his axioms are not consistent on a wider domain. Our characterisation, on the contrary, is robust to different -and, one could argue, more realistic- specifications of the domain (Theorem 4.2). This, we also argue, makes bargaining problems more directly comparable to standard social decision problems. In addition, the characterisation is showed to be robust to modifications of the axioms which could sensibly be required: (Corollary 3.3 and Theorem 5.2.1).
Finally, we also study a converse problem. Can an arbitrator who is, in some sense, rational be deemed to be also fair in the sense that he abides by the Suppes-Sen principle? We give a qualified positive answer, which depends on interpreting IIA and Pareto optimality as principles of rationality, and Symmetry as an informational constraint. We show that, on the domains of convex comprehensive or just comprehensive problems, in the presence of Symmetry, Pareto optimality and IIA imply that the choice must be SS-undominated (Theorem 5.2.1). In other words, an arbitrator who is rational in the sense specified above must behave as if he was taking into account the interpersonal ordinal utility comparisons implied by the Suppes-Sen principle. When the domain includes nonconvex problems, the same axioms yield in fact an even stronger property, namely full cardinal interpersonal comparability in the guise of Egalitarianism (Theorem 5.2.2).
In Nash's (1950) theory, an n-person bargaining problem is a pair (S,d), where S n and d S. The interpretation is that S is the set of feasible utilities attainable by the players and d is the disagreement point which results if no agreement is attained. In order to enhance expositional clarity, in the main text we make two simplifications:
(1) n = 2;
(2) d = 0 (0,0).
None of the results depends on (1). In the appendix we show in full how some definitions and the main result generalise. As will be apparent, nothing conceptual is lost by assuming (1) but much is gained in readibility. As for (2), this is a much used convention which saves on notation and is also immaterial, provided that the assumption of Scale Covariance made below is transformed to include, as usual, the weak requirement of translation covariance.
This allows us to describe a bargaining problem simply as a set S 2. Let be a collection of bargaining problems. Then a solution on is a function : 2 such that (S) S for all S . It is standard to impose the following restrictions on S:
A1) S is compact;
A2) S is convex;
A3) there exists s S such that s > 0.
Restriction (A2) in particular is not trivial; we shall see later how one of the advantages of our approach is that it can be dispensed with, allowing one to consider nonconvex or even discrete sets of feasible alternatives. Let denote the collection of all bargaining problems satisfying (A1) through (A3). Some standard properties that can be imposed on a solution are the following:
Weak Pareto Optimality (WPO): s > (S) s S.
Strong Individual Rationality (SIR): (S) > 0.
Covariance with Positive Scale Transformations (COV): let : 2 2 be a positive, linear, component by component transformation given by (x) = (1x1,2x2), with 1,2 > 0, for all x 2, and for any X 2 let (X) = {y 2| y = (x) for some x X}. Then, ((S)) = ((S)).
Symmetry (SYM): suppose that s S (s2,s1) S. Then, 1(S) = 2(S).
Anonymity (AN): let : 2 2 be a map such that (x) = (x2,x1) for all x 2. Then, ((S)) = ((S)).
Independence of Irrelevant Alternatives (IIA): S T and (T) S (T) = (S).
Some solutions that will be mentioned later are:
.
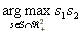For any X 2 let coX denote the convex hull of X. For all S , let ai(S) max{si | s S, s 0}. The point a(S) is called the ideal point.
Nash (1950) proved that the NBS is the only solution on that satisfies WPO, IIA, COV and SYM (or AN). We will refer to these four axioms as Nash's axioms. The KSS is sometimes identified with relative egalitarianism (see e.g. Moulin (1988)): it equalises the gains from the disagreement point of each player relative to the maximum possible such gain. It satisfies COV but not IIA. The ES simply equalises the gains from the disagreement point. It satisfies IIA but not COV, and hence it must be based on interpersonal (cardinal) utility comparisons, unlike the NBS and the KSS which do not require any interpersonal comparisons. Note finally how all three solutions satisfy both SYM and AN.
Given s,t 2, s is said to SS-dominate t if s > t or (s2,s1) > t. Suppose that it is logically meaningful (although not necessarily empirically possible) to make ordinal interpersonal comparisons of utility. Suppose that the utilities of the two players happen to be scaled with the same unit: in this case, whether or not the arbitrator has used such comparisons to determine a certain outcome, if that outcome is SS-dominated it can be reasonably argued to be unfair. If the arbitrator does not know whether the utilities are scaled with the same unit, he cannot know if he has been unfair or not, unless he chooses in such a way that, whatever the scaling, the outcome is not SS-dominated. This leads to the formulation of the following requirement for a solution function:
Suppes-Sen Proofness (SSP): (s2,s1) > (S) or s > (S) s S.
Clearly, SSP is a strengthening of WPO obtained by combining an 'anonymity' principle with the optimality principle. However, it goes far beyond the mere joining of the axioms of WPO and AN (or SYM)! As we noted before, all three solutions NBS, ES and KSS satisfy both WPO and AN. Full egalitarianism, as embodied by the ES, clearly also satisfies SSP. But relative egalitarianism, as embodied by the KSS, does not.
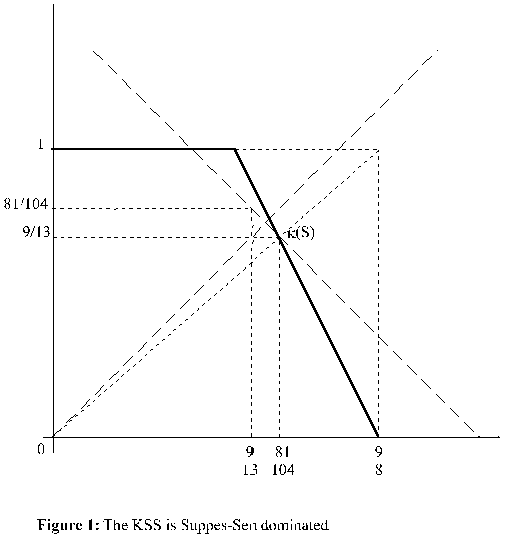
Example 3.1: S = co{0, (0,1), (5/8,1),(9/8,0)}.
We have (S) = (81/104,9/13). Let s = (29/40,4/5). Then, since
it is s S, 4/5 > 81/104 and 29/40 > 9/13, (S) is SS-dominated
(see Figure 1).
On the other hand, COV excludes the ES. This already shows how powerful SSP becomes when paired with COV. More in general, we have the following main result:
Theorem 3.2: a solution : 2 satisfies COV and SSP if and only if = .
Proof: given S , suppose that there existed s S with (s2,s1) > (S). Then also s1s2 > 1(S)2(S), a contradiction. This, together with the well-known facts that the NBS satisfies COV and WPO, proves the 'if' part of the statement.
For the 'only if' part, let S and suppose by contradiction that s (S) (S). We will show that then there exists T such that (T) is SS-dominated. If there exists t S with t > s we are done, so assume that s is weakly Pareto optimal. Distinguish three cases.
Case 1: s > 0. Given any point x 2++, let H(x) denote the branch of the symmetric hyperbula going through x, that is, H(x) = {y 2++| y1y2 = x1x2}. Clearly, there exists t H(s) such that (S) > t. Consider now a positive linear transformation defined by 1(s) = 2(t) and 1(t) = 2(s). Such a transformation is defined (not uniquely) by (x) = (1x1,2x2) for all x 2 where: 1,2 >0, 1\2 = t2\s1 = s2\t1. Since s,t H(s), these equations have a solution.
Let (S) T. We have ((S)) > (t) = (2(s),1(s)). Therefore (s) is SS-dominated by ((S)) in T, and by SSP it must be (s) (T). However, by COV it must be (T) = ((S)) = ((S)) = (s), a contradiction.
Case 2: s1 = 0 (the case s2 = 0 is treated analogously; note that it cannot be s = 0 if s is weakly Pareto optimal). Since (S) > 0, there exists > 0 such that (,0) < (S). Let 2 > 0 be such that 2s2 = . Define the transformation by (x) = (x1,2x2). Now the argument of the previous case applies to (S).
Case 3: s1 > 0, s2 < 0. Let t 2, with t1 < 0 and t2 > 0, be such such that s1s2 = t1t2. In addition, it is clearly possible to choose such a large negative value for t1 that t < (S). Again define 1,2 > 0 and as in case 1 and argue analogously.
Thus, choosing in accordance with the NBS is the only way for an arbitrator who has no information on the relative scaling of the players' cardinal utilities -that is, who only knows the equivalence class of cardinal utility functions- to make sure that no injustice is committed according to the Suppes-Sen principle.
In conclusion of this section, we note that the NBS satisfies a much stronger fairness criterion than SSP, related to second-order stochastic dominance (or Generalised Lorenz dominance). Given s,t 2, s is said to GL-dominate t if there exists [0,1] such that (s1 + (1-)s2, (1-)s1 + s2) > t. It is immediately verified that = 0 implies SS-dominance and that = 1 implies weak Pareto dominance (and hence SS-dominance).
Generalised Lorenz Proofness (GLP): (s1 + (1-)s2, (1-)s1 + s2) > (S), [0,1] s S.
It is easy to verify that the NBS cannot yield a GL-dominated outcome. By definition, the feasible set S is bounded above at (S) by the symmetric hyperbula through (S), H((s)). The set of points t = (1(S) + (1-)2(S), (1-)1(S) + 2(S)) with [0,1] is the segment joining (S) and (2(S),1(S)). This segment -connecting a point of H((s)) with another point which, being symmetric to the first, is also on H((s))- lies entirely above H((s)). Therefore for any point t that GL-dominates (S) it must be t S. Thus:
Corollary 3.3: let : 2 be a solution satisfying COV and SSP. Then it also satisfies GLP.
Thus, the informational constraint given by COV and the merely ordinal criterion of fairnes given by SSP force one to accept a substantially more stringent interpersonal comparability criterion: for, clearly, the concept of GL-domination requires full cardinal interpersonal comparability (see also Theorem 5.2.2 below).
This section contains some remarks on how the characterisation result of the previous section depends on the nature of the domain. The assumption that S is convex is justified by the fact that alternatives are expressed in von Neumann-Morgenstern utilities and that lotteries are available. These two requirements, although fairly standard, are not always palatable. If players are not expected utility maximisers, or if in some underlying game in strategic form no correlating device is available, or simply if players are not willing or able to randomise at all, the feasible set will not be convex or even a continuum. In addition, as Moulin (1996, p. 126) observes, "It is hard to believe that our search for operational criteria of fairness should be confined to a convex world".
Fortunately, the characterisation in terms of SSP given above is quite robust to variations of the basic setting. Since the set of maximisers of the Nash product is not necessarily a singleton when the domain is not convex, in this section we turn to multisolutions. Let be a collection of bargaining problems. Then a multisolution on is a correspondence : 2 such that (S) S for all S . The NBS viewed as a multisolution is defined analogously to the solution; the KSS and the ES are always single-valued when they are well-defined. Some axioms are redefined accordingly; a star indicates that they refer to multisolutions:
Weak Pareto Optimality (WPO*): s > t (S) s S.
Strong Individual Rationality (SIR*): s (S) s > 0.
Symmetry (SYM*): suppose that s S (s2,s1) S. Then, s (S) (s2,s1) (S).
Independence of Irrelevant Alternatives (IIA*): S T and (T) S (S) = (T) S.
Suppes-Sen Proofness (SSP*): (s2,s1) > t (S) or s > t (S) s S.
COV and AN remain unchanged.
We consider two interesting domains. The first is , the class of problems S that satisfy (A1) and (A3) in section 2 and such that, in addition, S is comprehensive ((A4) below):
A4) let s s' s''; then s, s'' S s' S.
The second domain is , the class of problems S that satisfy (A3) of section 2 and such that, in addition, S contains a finite number of alternatives. For comparison, we summarise next some results of Mariotti (1996a):
Theorem 4.1: there exists no solution : 2 that satisfies Nash's axioms. There esists however a multisolution : 2 that satisfies WPO*, COV, SYM* and IIA*. This multisolution is unique and it is the NBS. Finally, the NBS is also the only multisolution : 2 that satisfies these axioms.
Single-valuedness is thus incompatible with Nash's axioms. We also note that there exists no characterisation in terms of WPO*, COV, SYM* and IIA* for the NBS multisolution : 2 (Kaneko (1980) has a characterisation on this domain which involves also an upper-semicontinuity axiom). is the natural domain to consider when randomisations are available but the players are not necessarily expected utility maximisers (Rubinstein et al. (1992)), or they cannot correlate their strategies in the underlying strategic form description. is the natural domain to consider when randomisations are not available at all. In the present approach, we have:
Theorem 4.2: a multisolution : 2, with {, , }, satisfies COV and SSP* if and only if . In particular, there exist solutions : 2, with {, , }, which satisfy COV and SSP, and such solutions are all selections from the NBS.
Here, the notation means: (S) (S) for all S . The proof of this theorem uses the same argument used for theorem 3.1, so we will not repeat it here.
These results suggest that, unlike the standard characterisation, our new characterisation of the NBS is relatively independent of the precise structural properties of the feasible set in the domain (observe that Corollary 3.3 is equally robust to changes of domain). One of the main advantages of this feature is that it makes bargaining problems more directly comparable to standard social decision problems, in the following sense. In the latter type problem one typically has (see e.g. Sen (1970)) a given set X of 'physical' alternatives, and individual preferences on X are then allowed to vary. In traditional bargaining theory, to the contrary, also the set X must be allowed to vary; otherwise, one might not be able to obtain in the feasible domain the problems needed for the proof (e.g., in Nash's (1950) case, one needs a symmetric rectangle to apply IIA). Our characterisation overcomes this difficulty, because the only axiom which involves comparisons of different bargaining problems is COV: it is perfectly possible, then, to think of the set of physical alternatives as fixed.
So far we have considered SSP as a basic fairness desideratum, and have shown that it can replace IIA, which is more appropriately considered as a rationality desideratum for individual choice behaviour, in Nash's axiom system. In this section we briefly consider a converse problem, and study to what extent IIA implies that choices must implicitly be based on the interpersonal utility comparisons embodied in the Suppes-Sen criterion, or even stronger ones. The results proved so far show that SSP follows from the four Nash's axioms. On the other hand, IIA and WPO alone clearly do not imply SSP (for example, the solution that maximises the first player's utility in each problem satisfies IIA and WPO but not SSP). However, they do so in the presence of SYM, at least on the domains of convex comprehensive or just comprehensive problems. Let com denote the class of all problems satisfying (A1) through to (A4).
Theorem 5.1.1: let : 2, with {com, }, be a solution satisfying IIA, WPO and SYM. Then, it also satisfies SSP.
Proof: suppose not, and let S com be a problem such that s = (S) is SS-dominated. That is, there exists t S with t > s or t > (s2,s1). Consider the latter case. Define T = co{0,s,(s2,s1)}. By convexity and comprehensiveness, T S, and by IIA (T) = s. Since T is symmetric, by SYM s1 = s2. Then t > (s2,s1) implies t > s, contradicting WPO.
The proof for the case S proceeds analogously, by constructing T as the polygon of vertices 0, (0,si), (sj,si), (sj,sj), (si,sj) and (si,0) where i,j {1,2} and sj min{s1,s2}. In this case T S by comprehensiveness alone.
We also report a result communicated to us by J. Greenberg (proof available upon request), which strengthens theorem 5.1.1 for the domain and shows that in this case the arbitrator must explicitly make full cardinal interpersonal comparisons (recall that Corollary 3.3 required an implicit use of such comparisons, in the sense of respecting COV):
Theorem 5.1.2 (Greenberg): a solution : 2 satisfies IIA, WPO and SYM if and only if = .
One interesting, if not compelling, key to read these results is to view SYM as an informational constraint, rather than as a fairness requirement. When the feasible set is symmetric, there is nothing on the basis of which the arbitrator can possibly differentiate between the players, if he decides on the basis of utility information alone. Under this interpretation, theorem 5.1 says that an arbitrator who is thus constrained and who is 'rational' in the sense of abiding by IIA and WPO is also necessarily 'fair' in the Suppes-Sen sense.
It is evident from the proof of Theorem 3.2 that there is a great deal of freedom in the choice both of the point t and of the scale transformation . Accordingly, from the mathematical viewpoint, the theorem can be considerably strengthened. We note two such strengthenings which may be also conceptually relevant.
One potential objection to SSP is that, given a problem S and its solution (S), the alternative (2(S),1(S)) may not be feasible. In this case it could be asked: why should the issue of Pareto domination of a non-feasible alternative be of any bearing for the issue of arriving at a fair decision within the feasible set? Nonfeasible alternatives should be, to all effects, irrelevant. In other words, one might want to weaken SSP to:
SSP**: s > (2(S),1(S)) S or s > (S) s S.
However, replacing SSP with SSP** in the statement of Theorem 3.2 would not affect its validity. It is obvious, in fact, that one can choose for t the point of intersection between the segment joining 0 and (S) and the hyperbula on which s lies. Then, by convexity (or, in the nonconvex case, by comprehensiveness), t S. Summarising:
Theorem 5.2.1: a solution : 2 satisfies COV and SSP** if and only if = .
Further, it has sometimes been argued that COV is not as innocent as it looks (e.g. Kalai (1985), Rubinstein et al. (1992)). In the proof of Theorem 3.2 the coefficients 1 and 2 were only determined up to their ratio (see the Appendix for the generalisation of this statement to general n-player problems). Consequently, the class of transformations for which COV should hold can be restricted, and a new interpretation can be offered. Suppose, in particular, that we required 1 + 2 = 1. Then, COV could have the following interpretation. Given a feasible set S, consider a situation where only one of the two players gets his part of the arbitrated alternative (S), while the other gets nothing. In particular, with probability 1 only player 1 gets 1(S), and with probability (1-1) only player 2 gets 2(S). COV now requires that the decision of the arbitrator should be the same in this situation and in the standard one where both players can be satisfied.
In this paper we have supported and characterised the NBS as an expression of distributive justice. We emphasise in conclusion that this interpretation is only valid in circumstances when the axiomatic solution of a bargaining problem à la Nash can be held to be appropriate for issues of fairness. In particular:
i) there is one distinguished point (d) which is allowed to be relevant for solving the distributional problem;
ii) cardinal utility information is available;
iii) the decision can be made on the basis of utility information alone.
Sen (1970), for example, has discussed situations in which the disagreement point should have no bearing on justice issues (note, however, that the interpretation of d as disagreement point is not necessary; all that matters is that there exists a Pareto dominated point for which Arrow's Independence can be violated). If (ii) and (iii) are not good assumptions (e.g. Roemer (1986, 1990, 1996)), other methods and procedures for deciding fairly will be more useful (see e.g., Young (1994) and Brams and Taylor (1996)).
We believe that it is possible to justify (i), (ii) and (iii) in general, but in this paper we eschew a discussion which is more philosophical in nature. We make instead a minimal claim which should be uncontroversial: there exist situations where (i), (ii) and (iii) hold. For those cases, we hope to have shown that the NBS is the most appropriate way of resolving conflicts of interest fairly, being the only solution that reconciles two powerful yet conflicting needs: on the one hand, interpersonal comparisons of utility should be not used in its calculation; on the other hand, basic principles of fairness relying on such comparisons should not be violated by its outcomes.
All the definitions and arguments for the results of the text generalise easily to the n-person case. In this appendix, by way of illustration, the definitions of SSP and GLP and the proof of Theorem 3.2, which is the least straightforward to generalise, are given. The generalisations of domains, standard axioms and solutions are obvious. Given s,t n, s is said to SS-dominate t if As > t for some permutation matrix A; s is said to GL-dominate t if As > t for some bistochastic matrix A.
Suppes-Sen Proofness (SSP): As > (S) for some permutation matrix A s S.
Generalised Lorenz Proofness (GLP): As > (S) for some bistochastic matrix A s S.
Theorem A.3.2: A solution : n satisfies COV and SSP if and only if = .
Proof: 'If': We note a stronger property of , namely that it satisfies GLP. That this is so follows from the fact that the Nash product is a symmetric increasing concave function and from standard characterisation results available in the literature.
'Only if': let S and suppose by contradiction that s (S) (S). We will show that then there exists T such that (T) is SS-dominated. If there exists t S with t > s we are done, so assume that s is weakly Pareto optimal (hence, in particular, not s 0). Distinguish three cases.
Case 1: s > 0. Given any point x n++,
let H(x) denote the symmetric hyperboloid going through x, that
is, H(x) = {y n++|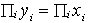 
}.
Clearly, there exists t H(s) such that (S) > t. In addition
it is possible to choose t so that ti si
for all i {1,2,...,n}. Consider now a positive linear transformation
defined by (s) = A(t), where A is the nn permutation matrix
which moves the ith component to the (i+1)th
place (setting n+1 = 1). That is:
A 
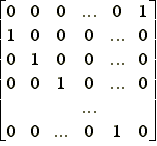
We show that such a transformation exists (not uniquely). Denote S and T the nn diagonal matrices with the components of s and t, respectively, on their diagonal, and denote the n1 vector of coefficients representing (that is, i(x) ixi for all x n, i {1,2,..,n}). It must be proved that the homogeneous system:
(A1) S = AT
has (a class of) strictly positive solutions in . (A1) has nontrivial solutions if and only if:
(A2) |S - AT| = 0.
We have:
K S - AT =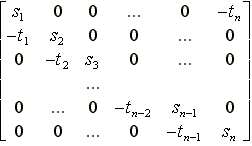 
Expanding along the first row:
(A3) |K| = s1|M11| + (-1)n+1(-tn)|M1n|,
where Mij denotes the minor of K obtained by
removing the ith row and jth column. By
the properties of triangular matrices (e.g. Birkhoff and MacLane
(1953), p. 303), |M11| =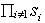 
and |M1n| = 
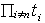. Note that
the second term on the RHS of (A3) is negative for all n. Therefore
(A2) holds if and only if 
=
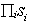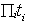or, equivalently, if and only if t H(s). Since t was chosen exactly
in this way, (A1) has nontrivial solutions.
Suppose now that * is a nontrivial solution of (A1) and that *i < 0 (resp. = 0) for some i {1,2,...,n}. This means (by inspection of K and the fact that s,t > 0) that *i-1 < 0 (resp. = 0). Consequently, *i < 0 (resp. = 0) for all i {1,2,...,n}. The case * = 0 is excluded by nontriviality. If * < 0, then -* > 0 is also a solution. We conclude that the desired exists in this case.
Now let (S) T. We have ((S)) > (t) = A-1(s). Therefore A((S)) > (s), and by SSP it must be (T) (s). However, by COV it must be (T) = ((S)) = ((S)) = (s), a contradiction.
Case 2: There exists I {1,2,...,n} with si = 0 for i I and si > 0 for i {1,2,...,n}\I. Without loss of generality, write s (possibly relabeling the axes) in such a way that the first k components are positive and the other negative: that is, let k be such that si > 0 for 1 i k and si = 0 for k < i n. Now let t n have components with signs as follows : ti > 0 for 1 i < k and i = n; ti = 0 for k i < n. In addition, let t < (S) (this is possible since (S) > 0). Define the system (A1) as in case 1. The matrix K now has one or more rows whose entries are all zero (certainly the last row, since tn-1 = sn = 0), therefore (A1) has nontrivial solutions. If * is a nontrivial solution, by the choice of sign of t we now have that i-1\i = si\ti-1 whenever si > 0 (and hence ti-1 > 0). Therefore the *i have all the same sign for 1 i k. Since the other *i, k < i n, are all free variables, the choice * > 0 is certainly allowed, and the proof for this case concludes as in case 1.
Case 3: There exists I {1,2,...,n} with si < 0 for i I and si > 0 for i {1,2,...,n}\I. Without loss of generality, let k be such that si > 0 for 1 i k and si < 0 for k < i n. Define s' (s1,s2,...,sk-1,-sk,-sk+1,...,-sn-1,sn). Let t n have the following properties:
(a) sign ti = sign s'i;
(b)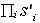 
=
;
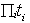(c) t < (S).
Given (b), (c) is possible by making the negative components of t sufficiently large in absolute value. At this point the argument proceeds in a way analogous to case 1 and will not be repeated.
Observation: By reduction (using induction) to echelon form of K it is easy to see that in fact the null-space of K in case 1 has dimension 1 for all n. The transformation is therefore subject to exactly the same degree of freedom as in the two-person case, and the observations about the role of COV made in section 5.2.2 for that case apply here as well.
Arrow, K.J. (1951) "Social choice and individual values", Wiley, New York.
Arrow, K.J. (1959) "Rational choice functions and orderings", Economica 26: 121-27.
Binmore, K. (1992) "Fun and games", D.C. Heath and Company, Lexington, Ma.
Birkhoff, G. and S. MacLane (1953) "A survey of modern algebra", MacMillan, New York.
Blackorby, C and D. Donaldson (1977) "Utility vs. equity: some plausible quasi-orderings", Journal of Public Economics 7: 365-81.
Blackorby, C., W. Bossert and D. Donaldson (1994) "Generalized Ginis and cooperative bargaining solutions", Econometrica 62: 1161-1178.
Blackorby, C., W. Bossert and D. Donaldson (1996) "Consistency, replication invariance and Generalized Gini bargaining solutions", Journal of Economic Theory 69: 367-86.
Bossert, W. (1994) "Rational choice and two-person bargaining solutions", Journal of Mathematical Economics 23: 549-63.
Brams, S. and A. Taylor (1996) "Fair division", Cambridge University Press, Cambridge.
Conley, J.P. and S. Wilkie (1996) "An extension of the Nash Bargaining Solution to nonconvex problems", Games and Economic Behaviour 13: 26-38.
Elster, J. and J.E. Roemer (1991) "Interpersonal comparisons of well-being", Cambridge University Press, Cambridge.
Fernandez, R. and J. Glazer (1991) "Striking for a bargain between two completely informed agents", American Economic Review 81: 240-52.
Gauthier, D. (1986) "Morals by agreement", Oxford University Press, Oxford.
Gauthier, D. and R. Sugden (eds.) (1993) "Rationality, justice and the social contract", Harvester Wheatsheaf, Hemel Hempstead.
Haller, H. and S. Holden (1991) "A letter to the editor on wage bargaining", Journal of Economic Theory 52: 232-36.
Hammond, P.J. (1991) "Interpersonal comparisons of utility: Why and how they are and should be made", ch. 7 of Elster and Roemer.
Herrero, M.J. (1989) "The Nash program: non-convex bargaining problems", Journal of Economic Theory 49: 266-77.
Jevons, W.S. (1871) "The theory of political economy", Macmillan, London.
Kalai, E. (1977) "Proportional solutions to bargaining situations: interpersonal utility comparisons", Econometrica 45: 1623-30.
Kalai, E. (1985) "Solutions to the bargaining problem", in: L. Hurwicz, D. Schmeidler and H. Sonnenschein (eds.), "Social goals and social organisations: Essays in memory of E. Pazner", Cambridge University Press, Cambridge.
Kalai, E. and M. Smorodinsky (1975) "Other solutions to Nash's bargaining problem", Econometrica 43: 510-18.
Kaneko, M. (1980) "An extension of the Nash bargaining problem and the Nash social welfare function", Theory and Decision 12: 135-48.
Kolm, S-C. (1971) "Justice et equite", CEPREMAP, Paris.
Krishna, V. and R. Serrano (1996) "Multilateral bargaining", Review of Economic Studies 63: 61-80.
Lensberg (1988) "Stability and the Nash solution", Journal of Economic Theory 45: 330-41.
Madden, P. (1996) "Suppes-Sen dominance, generalised Lorenz dominance and the welfare economics of competitive equilibrium: Some examples", Journal of Public Economics 61: 247-62.
Mariotti, M. (1994) "The Nash solution and Independence of Revealed Irrelevant Alternatives", Economics Letters 45, 175-79.
Mariotti, M. (1996a) "Nash Bargaining Theory when the number of alternatives can be finite", mimeo, University of Manchester.
Mariotti, M. (1996b) "A model of agreements in strategic form games", Journal of Economic Theory, forthcoming.
Mas Colell, A., M.D. Whinston and J.R. Green (1995) "Microeconomic theory", Oxford University Press, New York and Oxford.
Moulin, H. (1988) "Axioms of cooperative decison making", Cambridge University Press, Cambridge.
Moulin, H. (1996) "Stand alone and Unanimity tests: A re-examination of fair division", in F. Farina, F. Hahn and S. Vannucci (eds.) "Ethics, rationality and economic behaviour", Clarendon Press, Oxford.
Myerson, R. (1981) "Utilitarianism, egalitarianism and the timing effect in social choice problems", Econometrica 49: 883-97.
Myerson, R. (1990) "Game theory. Analysis of conflict", Harvard University Press, Cambridge, Ma.
Nash, J.F. (1950) "The bargaining problem", Econometrica 18: 155-62.
Peters, H.J.M. (1992) "Axiomatic bargaining game theory", Kluwer Academic Publishers, Dordrecht.
Peters, H.J.M. and P. Wakker (1991) "Independence of Irrelevant Alternatives and revealed group preferences", Econometrica 59: 1787-801.
Ray, D. and R. Vohra, "Equilibrium binding agreements", Brown University, Department of Economics Working Paper 92-8 (1992).
Robbins, L. (1932) "An essay on the nature and significance of economic science", Macmillan, London.
Roemer, J.E. (1986) "The mismarriage of bargaining theory and distributive justice", Ethics 97: 88-110.
Roemer, J.E. (1990) "Welfarism and axiomatic bargaining theory", Recherches Econmiques de Louvain 56: 287-301.
Roemer, J.E. (1996) "Theories of distributive justice", Harvard University Press, Cambridge, Mass.
Roth, A. (1979a) "Axiomatic models of bargaining", Springer Verlag, Heidelberg.
Roth, A. (1979b) "Proportional solutions to the bargaining problem", Econometrica 47: 775-78.
Rubinstein, A., Z. Safra and W. Thomson (1992) "On the interpretation of the Nash Bargaining Solution and its extension to non-expected utility preferences", Econometrica 60: 1171-86.
Sànchez-Antòn, M.C. (1996) "Rationality of bargaining solutions", University of Alicante Working Paper A discusion # 96-09.
Saposnik, R. (1983) "On evaluating income distributions: rank-dominance, the Suppes-Sen Grading Principle of Justice and Pareto Optimality", Public Choice 40: 329-36.
Sen, A. (1970) "Collective choice and social welfare", Holden-Day, san Francisco.
Shorrocks, A. (1983) "Ranking income distributions", Economica 50: 3-18.
Suppes, P. (1966) "Some formal models of grading principles", Synthese 6: 284-306.
Thomson, W. (1990) "The consistency principle", in T. Ichiishi, A. Neyman and Y. Tauman (eds.), "Game theory and applications", Academic Press, san Diego.
Thomson, W. (1995) "Cooperative models of bargaining", in R. Aumann and S. Hart (eds.), Handbook of Game Theory, Vol 2, North Holland, Amsterdam.
Thomson, W. and T. Lensberg (1989) "Axiomatic theory of bargaining with a variable number of agents", Cambridge University Press, Cambridge.
Weymark, J.A. (1991) "A reconsideration of the Harsanyi-Sen debate on utilitarianism", ch. 8 of Elster and Roemer (1991).
Young, H.P. (1994) "Equity in theory and practice", Princeton University Press, Princeton, NJ.
Zhou, L. (1996) "Nash bargaining theory and the revealed preference theory for non-convex problems", Econometrica, forthcoming.
