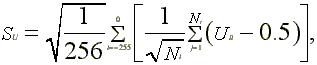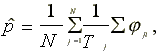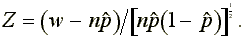Trading Frequency and Event Study Test
Specification*
Arnold R. Cowan
Department of Finance
Iowa State University
Ames, Iowa 50011-2063
(515) 294-9439
arnie@iastate.edu
Anne M.A. Sergeant
Department of Accounting
Iowa State University
Ames, Iowa 50011-2063
(515) 294-2204
anne_sgt@iastate.edu
This draft: January 1996
Forthcoming, Journal of Banking
& Finance
We examine the effects of thin trading on the specification
of event study tests. Simulations of upper and lower tail tests
are reported with and without variance increases on the event
date across levels of trading volume. The traditional standardized
test is misspecified for thinly traded samples. If return variance
is unlikely to increase, then Corrado's rank test provides the
best specification and power. With variance increases, the rank
test is misspecificed. The Boehmer et al. standardized
cross-sectional test is properly specified, but not powerful,
for upper-tailed tests. Lower-tailed alternative hypotheses can
best be evaluated using the generalized sign test.
JEL classification: G14
Keywords: event study
research methods; trading volume; thin trading;
nonparametric tests; Nasdaq
*The authors are grateful to James Larsen, Nandkumar
Nayar, Ajai Singh, David Suk and two anonymous referees for helpful
comments.
- Introduction
The use of daily data in event studies is important
for isolating stock price reactions to announcements. A potential
problem with the use of daily returns is that thin trading may
cause statistical tests to be poorly specified. The issue of thin
trading is increasingly relevant as researchers use more daily
data from markets with wide ranges of trading frequency such as
the Nasdaq Stock Market. The frequency with which stocks are traded
is potentially important to the correct selection of test procedures.
This paper provides direct empirical evidence of the effect of
trading frequency on event study test specification and recommends
appropriate procedures for thinly traded samples.
Some properties of infrequently traded securities
are likely to differ from more heavily traded securities, and
these have implications for event study methods. Thinly traded
stocks are more likely to be characterized by numerous zero and
large non-zero returns, resulting in non-normal return distributions.
Cowan (1992) and Campbell and Wasley (1993) report substantial
departures from normality in the abnormal returns of Nasdaq stocks.
These authors also document that Nasdaq stocks exhibit a much
higher frequency of zero returns than New York and American Stock
Exchange stocks. Campbell and Wasley argue that the high frequency
of zero returns, and corresponding extreme nonzero returns, distort
the variance estimates required for the popular standardized abnormal
return test [Patell (1976)]. Infrequently traded securities are
more affected by nonsynchronous return periods for the stock and
market index. Scholes and Williams (1977) and Dimson (1979) demonstrate
that ordinary least squares estimates of market model parameters
are biased and inconsistent in the presence of nonsynchronous
trading. Institutional trading requirements (trading frictions)
can have different effects on the measurement error associated
with a security's return depending on trading volume. When trading
frictions are relatively higher, as in the case of trades being
made in eighths of a dollar for low priced securities, information
may not be acted upon until the gains exceed the costs. These
price adjustment delays enhance serial cross-sectional dependence
in observed returns which contribute to biased OLS beta estimates.
The longer the price adjustment delay, the more the OLS beta tends
toward zero [Cohen, Maier, Schwartz and Whitcomb (1986)].
Recent studies find a conventional parametric test
statistic, the Patell (1976) standardized abnormal return statistic,
poorly specified with thinly traded samples. Campbell and Wasley
(1993) report that the standardized test rejects a true null hypothesis
too often with Nasdaq samples. Maynes and Rumsey (1993) report
a similar misspecification of the test using the most thinly traded
one-third of Toronto Stock Exchange (TSE) stocks.
Three potential solutions to the problems of nonnormality
and misestimation of variance caused by thin trading appear in
the literature. Boehmer, Musumeci and Poulsen (1991) develop a
standardized cross-sectional test as a remedy for event-induced
increases in return variance. Their standardized cross-sectional
test retains the properties of the Patell standardized test in
adjusting for both non-constant variance across stocks and out-of-sample
prediction. The standardized cross-sectional test improves on
the Patell test by allowing the abnormal return variances to differ
between the estimation and event periods. Because trading activity
and therefore variance are likely to differ between the estimation
and event periods, the Boehmer, Musumeci and Poulsen procedure
is potentially useful in thinly traded samples.
A second potential solution for thinly traded stocks
is the rank test [Corrado (1989)]. The rank test is nonparametric
and therefore does not depend on the assumption of normality.
Campbell and Wasley (1993) report that the rank test is better
specified with Nasdaq data than common parametric tests. On the
other hand, Cowan (1992) finds that the rank test is misspecified
with Nasdaq data. Thus, the suitability of the rank test for thinly
traded samples is an unsettled question.
The third test is the generalized sign test analyzed
by Cowan (1992). Like the rank test, it is nonparametric, thus
avoiding the dependence on normality of return distributions.
It also exploits the large number of zero returns in Nasdaq samples
to improve power. Cowan reports the test to be well specified
in general samples from NYSE-AMEX and Nasdaq stocks.
As Campbell and Wasley (1993) observe, Nasdaq stocks
on average are smaller and less frequently traded than exchange-listed
stocks. However, some Nasdaq stocks are actively traded while
some exchange-listed stocks are thinly traded. The relative performance
of the standardized (Patell), standardized cross-sectional, rank,
and generalized sign tests could vary more across different levels
of trading activity than a comparison between NYSE-AMEX and Nasdaq
reveals. The present study takes advantage of the recent addition
to the CRSP files of daily trading volume data for both exchange-traded
and Nasdaq stocks. By using volume, we identify stocks that are
thinly traded and compare test statistics at different trading
frequencies. No previous study has examined the effect of thin
trading on the power and specification of event study test statistics
using daily volume data.
This paper reports simulations of event study tests
on exchange listed and Nasdaq stocks by deciles of trading volume.
The results show serious misspecification of the Patell standardized
test in thinly traded NYSE-AMEX samples and thinly to moderately
traded Nasdaq samples without an increase in return variance,
and in all samples with an increase in return variance. Of the
remaining tests, no one test is best across all situations. Even
with the most thinly traded stocks, the nonparametric generalized
sign and rank tests generally perform well as long as there is
no variance increase. If anything, the nonparametric tests detect
abnormal returns more often with thinly traded samples than with
heavily traded stocks. Of the two, the generalized sign test typically
is more powerful at detecting a positive abnormal return in thinly
traded NYSE-AMEX samples and all but the most actively traded
decile of Nasdaq stocks. The rank test is more powerful in the
remaining samples. The standardized cross-sectional test is well
specified with upper-tailed tests but less powerful than the nonparametric
tests. It also tends to commit too many Type I errors in lower-tail
tests.
When we simulate an increase in the return variance
on the event date, the standardized cross-sectional, rank and
generalized sign tests all exhibit misspecification in some samples.
The standardized cross-sectional test is correct for upper-tail
tests and the generalized sign test is correct for lower-tail
tests. However, if the suspected variance increase does not occur,
the researcher using these tests loses the superior power of the
rank test. In addition, we document that there is no pervasive
advantage to the adjustment of betas for thin trading.
- Experimental Design
The simulation approach used in this paper resembles
that of Brown and Warner (1985). Unlike a true Monte Carlo simulation
where the investigator samples artificially generated values from
a carefully specified theoretical probability distribution, Brown
and Warner repeatedly sample actual returns from the CRSP stock
files. By randomly selecting event dates and stocks, Brown and
Warner create simulated event studies without assuming a particular
distribution of stock returns. Similar research designs appear
in Corrado (1989), Boehmer, Musumeci and Poulsen (1991), Corrado
and Zivney (1992), Cowan (1992), and Campbell and Wasley (1993),
among others.
- Abnormal Returns
Abnormal returns are prediction errors from the market
model, 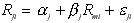 , where
, where 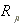 is the rate of return of the
is the rate of return of the 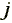 th stock
on day
th stock
on day 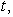 and
and 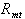 is
the rate of return of the CRSP NYSE-AMEX equally weighted market
index on day
is
the rate of return of the CRSP NYSE-AMEX equally weighted market
index on day 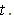 The random noise term
The random noise term 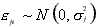 for
for 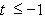 and
and 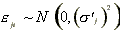 for
for
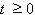 is assumed not to be autocorrelated.
The period for the estimation of the market model parameters is
days -255 through -1, where day 0 is the randomly selected event
date. Initially we assume that
is assumed not to be autocorrelated.
The period for the estimation of the market model parameters is
days -255 through -1, where day 0 is the randomly selected event
date. Initially we assume that 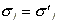 . Although
beta estimation is not the primary focus of the study, betas are
computed using both OLS and the Scholes and Williams (1977) procedure
that adjusts for the effect of thin trading on the market index.
The computation of Scholes-Williams betas requires additional
simple linear regressions of
. Although
beta estimation is not the primary focus of the study, betas are
computed using both OLS and the Scholes and Williams (1977) procedure
that adjusts for the effect of thin trading on the market index.
The computation of Scholes-Williams betas requires additional
simple linear regressions of  on lagged
and leading values of
on lagged
and leading values of 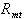 and the estimation
of the first-order autocorrelation of
and the estimation
of the first-order autocorrelation of 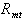 .
.
- Test Statistics
Following Boehmer, Musumeci and Poulsen (1991), we
use the following notation to describe the test statistics:
|
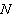 | number of stocks in the sample
|
|
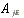 | stock j's abnormal return on the event day
|
|
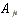 | stock j's abnormal return on day t
|
|
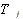 | number of trading days in stock j's estimation period, equal to 255 if there is no missing return
|
|
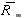 | average market index return during the estimation period
|
|
 | stock j's estimated standard deviation of abnormal return during the estimation period
|
|
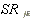 | stock j's standardized abnormal return on the event day

|
|
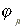 | =1 if
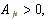 =0 otherwise =0 otherwise
|
|
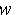 | number of stocks in the sample with a positive abnormal return on the event date
|
The test statistics examined are the Patell (1976) standardized
residual test studied by Brown and Warner (1985), the standardized
cross-sectional test introduced by Boehmer, Musumeci and Poulsen
(1991), the rank test introduced by Corrado (1989), and the generalized
sign test analyzed by Cowan (1992). The null hypothesis for each
test is that the mean abnormal return is equal to zero.
The Patell test standardizes the event-date prediction error for
each stock by its standard deviation. The individual prediction
errors are assumed to be cross-sectionally independent and distributed
normally, so each standardized prediction error has a Student
t distribution. By the Central Limit Theorem, the distribution
of the sample average standardized prediction error is normal.
The resulting test statistic is
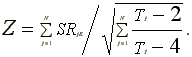
Brown and Warner (1985) report that the test is well specified
under the null hypothesis and more powerful than tests that do
not assume cross-sectional independence. However, if the variance
of stock returns increases on the event date, the Patell test
rejects the null hypothesis more often than the nominal significance
level.
In using Scholes-Williams betas with the Patell test, this paper
follows Moore, Peterson and Peterson (1986) by defining the standard
deviation of the prediction error the same way as with OLS betas.
Scholes-Williams and OLS prediction errors are different, so they
have different standard deviations. However, no adjustment is
made to the standard deviation formula specifically to reflect
the use of the lagged and leading market returns in the beta estimation.
This is consistent with the idea that, in the Scholes-Williams
procedure, the adjustment of beta should capture the true sensitivity
of the stock return to the contemporaneous market return. Thus,
only the contemporaneous market return on the event date, not
the lag or lead, enters the calculation of the prediction error.
Likewise, only the contemporaneous market return enters the calculation
of the standard deviation of the prediction error.
The standardized cross-sectional test is similar to the Patell
standardized test. The difference is that instead of using the
theoretical variance of the t distribution, the variance
is estimated from the cross-section of event-date standardized
prediction errors. The procedure requires the assumption that
the event date variance is proportional to the estimation period
variance: 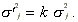 Boehmer, Musumeci and Poulsen
(1991) write the test statistic as
Boehmer, Musumeci and Poulsen
(1991) write the test statistic as
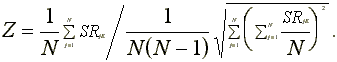
Boehmer, Musumeci and Poulsen report that the test is correctly
specified in NYSE-AMEX samples under the null hypothesis even
when there is a variance increase on the event date. Moreover,
unlike other prevalent tests, the standardized cross-sectional
test is nearly as powerful as the Patell test when there is no
variance increase.
The third test is the rank test developed by Corrado (1989). The
rank test procedure treats the 255-day estimation period and the
event day as a single 256-day time series, and assigns a rank
to each daily return for each firm. Following the notation of
Corrado, let Kjt represent the rank of abnormal
return ARjt in the time series of 256 daily
abnormal returns of stock j. Rank one signifies the smallest
abnormal return. Following Corrado and Zivney (1992), we adjust
for missing returns by dividing each rank by the number of non-missing
returns in each firm's time series plus one:
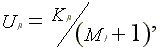
where 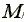 is the number of non-missing abnormal
returns for stock j. The rank test statistic is
is the number of non-missing abnormal
returns for stock j. The rank test statistic is
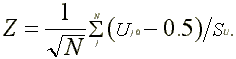
The standard deviation 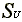 is
is
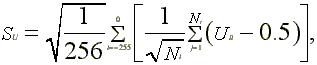
where there are Nt nonmissing returns across
the stocks in the sample on day t of the combined estimation
and event period. Corrado, Corrado and Zivney and Campbell and
Wasley (1993) report that the rank test is well specified and
powerful. Cowan (1992) reports the test to be powerful and well
specified with exchange-listed stocks, but misspecified for Nasdaq
stocks and when the return variance increases on the event date.
The fourth test is the nonparametric generalized sign test. This
test is like the traditional sign test. However, the sign test
requires the assumption that the number of stocks in a sample
of size n that have positive returns on the event date
follows a binomial distribution with parameter p. The null
hypothesis for the traditional sign test is that p=0.5.
In the generalized sign test, the null hypothesis does not specify
p as 0.5, but as the fraction of positive returns computed
across stocks and across days in the parameter estimation period.
Thus the fraction of positive abnormal returns expected under
the null hypothesis is
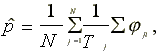
and the generalized sign test statistic is
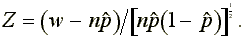
Cowan (1992) reports that the test is well specified and powerful
under a variety of conditions. Like the standardized cross-sectional
test, it is relatively robust to variance increases on the event
date.
- Sample Selection
- General Simulation Samples
The simulation samples come from the CRSP NYSE-AMEX and Nasdaq
daily stock return files. The NYSE-AMEX file contains returns
for all firms listed on the New York Stock Exchange or the American
Stock Exchange from July 1962 through December 1993. The Nasdaq
file contains returns from December 1972 through December 1993.
The samples contain 50,000 stock-event date combinations each
from the NYSE-AMEX and Nasdaq CRSP files. Within each of the two
CRSP files, we randomly select with replacement from stocks that
have at least 260 trading days of returns. The probability of
a stock being selected increases with the number of trading days
present on the file. For each stock selected, an event date is
randomly chosen with replacement from the range of dates that
returns are available for the stock. To allow for estimation,
the event date must occur after the first 255 trading days of
data for the stock. Subject to this constraint, all firm-event
day combinations present in the CRSP population are approximately
equally likely to enter the simulation sample.
If a stock has more than 12 missing returns in the estimation
period, another randomly selected stock (with a new event date)
takes its place. The elimination of stocks with many missing returns
does not necessarily exclude thinly traded stocks. Returns on
the CRSP files are computed from the average of ask and bid prices
when no closing trade price exists. Thus, even on a day when there
is no trade, there need not be a missing return.
The final 50,000 stock-event date combinations from each CRSP
file are grouped into 1000 NYSE-AMEX samples and 1000 Nasdaq samples
of 50 stocks. The grouping occurs in the same order as the random
draw.
- Volume-Clustered Samples
To gauge the effect of trading frequency on the specification
and power of event study tests, we need a measure of the trading
activity of the stock. Maynes and Rumsey (1993) use the mean number
of days between trades for their TSE sample. The reciprocal measure,
the number of trades per day, is available on the CRSP files only
for stocks on the Nasdaq National Market, which trade more actively
than Nasdaq Small-Cap Market stocks. (Current versions of the
CRSP files include the number of trades for Nasdaq Small-Cap stocks
from mid-1992 onward, making only a year and a half of data available
to this study.) However, CRSP reports the daily volume of shares
traded for the two Nasdaq markets and for NYSE-AMEX stocks. We
measure the trading activity for each stock by the mean shares
traded over the 255-day estimation period.
The ranking of stocks by trading volume should produce results
similar to ranking by the number of trades per day. To verify
this claim, we randomly select 2,500 stock-event date combinations
from the Nasdaq file using an algorithm similar to the one that
selected the initial samples for the main simulations. We compute
the mean volume and number of trades over a 100-day period beginning
with the randomly selected date. The Spearman rank correlation
between the mean number of trades and the mean volume is 0.93
(p-value = .001). The 100-day mean number of trades ranges from
0.12 to 618.88 trades per day, with a grand mean of 20 and a median
of 7 trades per day. We conclude that volume is a good measure
of trading frequency.
To construct volume-clustered samples,
800,000 NYSE-AMEX and 800,000 Nasdaq stock-event date combinations
are drawn as described above. After we impose a requirement of
at least 50 days of volume data in the estimation period, 796,777
NYSE-AMEX and 601,371 Nasdaq stock-event date combinations survive.
The large number of dropouts from the Nasdaq sample occurs because
no volumes are available on the CRSP file for any Nasdaq stocks
before November 1982. We sort the combinations into decile groups.
Each decile group contains more than 50,000 stock-event date combinations,
so we randomly select combinations from the decile groups for
simulation purposes. Table 1 reports the mean, minimum and maximum
volume for the full decile groups 1-10. To examine the performance
of event study methods with thinly traded samples in comparison
to actively traded stocks, we run simulations on the decile groups.
- Simulating Abnormal Performance
We follow Brown and Warner (1985) in simulating abnormal performance
by adding a constant to each day 0 (event date) actual stock return.
The simulations are repeated with a constant of zero or positive
or negative 0.5%, 1% or 2%.
- Results
- Distributional properties of abnormal returns under the null
hypothesis
Table 2 reports summary statistics of abnormal returns over the
255-day estimation period for the 50,000 stocks in each of the
22 simulation samples. The table reports the average of 50,000
stock-specific time-series means, standard deviations, skewness,
centered kurtosis coefficients, and studentized ranges.
The daily abnormal returns of Nasdaq stocks depart from normality
to a greater degree than NYSE and AMEX stocks. Both are positively
skewed and leptokurtic, and studentized ranges exceed 7.7, well
outside a 95% confidence interval for a normal population. For
both NYSE-AMEX and Nasdaq stocks, nonnormality increases as trading
frequency decreases. Nasdaq decile 1 exhibits particularly severe
departures from normality with the kurtosis coefficient exceeding
26 and the studentized range close to 11. The standard deviation
in this decile is smaller than more actively traded samples. These
characteristics are consistent with a high proportion of zero
returns, which would be expected in such a profoundly thinly traded
sample.
Table 3 reports statistics of the cross-sectional distributions
of day 0 (event day) portfolio abnormal returns for the 1000 50-stock
portfolios in each of the 22 samples. Combining stocks into portfolios
produces smaller departures from normal return distributions.
Skewness and kurtosis values exceed normal benchmarks in all cases.
Skewness coefficients range from less than 0.40 for actively traded
NYSE-AMEX stocks to about 0.60 for some Nasdaq samples. Kurtosis
coefficients exceed 6.5 for all samples and are over 13 for the
most thinly traded Nasdaq stocks. However, the studentized range
values are within the 95% confidence interval for a normal population.
- Tests with No Change in the Return Variance
Table 4 reports the simulation results for exchange-listed stocks
at 5% and 1% nominal significance levels in panels A and B respectively.
When the artificially induced abnormal return is zero, the tests
should reject the null hypothesis of no abnormal performance 5%
and 1% of the time. When no variance change is induced, the rejection
rates of all four tests under the null for both the upper and
lower-tails are mostly within the 95% confidence interval. The
only exception is the standardized cross-sectional (OLS) lower
tailed test, which is at the 95% significance level. Thus, misspecification
is not identified for any of the four test statistics for the
NYSE-AMEX stocks.
Brown and Warner (1985, table 8) report an OLS upper-tailed rejection
rate of 6.4% for the Patell test under the null hypothesis. This
is larger than the 5.4% reported in table 4 panel A; however,
both are larger than the expected value of 5.0%. The standardized
cross-sectional test rejects 4.6% of the time for the upper tail
and 6.4% for the lower tail. These results are consistent with
those of Boehmer, Musumeci and Poulsen (1991), who report an upper-tailed
rejection rate of 4.8%. The generalized sign test is well specified
in the lower tail, which is consistent with Cowan (1992).
There is no noticeable improvement in the power of the tests using
Scholes-Williams betas. For some tests at some abnormal return
levels, the power is greater, while for other combinations, it
is lower or unchanged. Thus, for exchange-listed stocks, there
is no apparent advantage to the use of Scholes-Williams betas.
This is the conclusion that Brown and Warner (1985) and Dyckman,
Philbrick and Stephan (1984) also reach.
Each of the test statistics, with the exception of the generalized
sign, shows similar power between the upper and lower-tails. The
rejection rates for the generalized sign test typically are 13
percentage points better for the upper-tail tests as compared
to the lower-tailed tests. This occurs because the generalized
sign test compares the percentage of positive abnormal returns
on the event date to the percentage in the estimation period.
Because the percentage of positive abnormal returns in the estimation
period is less than 50% due to the presence of zero raw returns,
the power to detect negative abnormal returns is lower.
Table 5 reports the corresponding results for Nasdaq stocks. The
upper-tailed Patell standardized test is the only one that has
a rejection rate that exceeds the upper 95% confidence limit for
no induced abnormal return. It rejects the true null hypothesis
8.6% of the time at 5% level and 3.6% of the time at 1% level,
both of which are outside a 99% confidence interval. The rejection
rate at 5% level is consistent with the 9.6% reported by Campbell
and Wasley (1993) and suggests misspecification for the more thinly
traded Nasdaq sample. The power of the generalized sign test is
greater for the upper-tail than the lower-tail tests. Like the
exchange listed results, the use of Scholes-Williams betas did
not improve the power of the test statistics. This conclusion
also is consistent with Campbell and Wasley.
The power of the tests with Nasdaq samples is roughly similar
to their power in exchange-listed samples when the artificially
induced abnormal return is 2%; all of the tests show rejection
rates of 97% or better. The nonparametric tests are more powerful
than the parametric tests for both samples at each artificially
induced abnormal return.
- Tests with a Variance Increase on the Event
Date
Brown and Warner (1985) report that variance increases on the
event date cause tests that use estimation period data to reject
the null hypothesis too often. Boehmer, Musumeci and Poulsen (1991)
report that the standardized cross-sectional test offers better
specification in cases of variance increases. We use the same
method as Brown and Warner (1985) to simulate an increase in the
raw return variance on the event date. Assume that the day 0 and
day +5 returns, as drawn from the CRSP file, are independent and
identically distributed, with the same expected value as a return
in the pre-event estimation period. Given the random selection
of stocks and event dates, the assumption is reasonable. Then
the following procedure will double the variance of the day 0
return without changing its expected value. For each stock, we
add the day +5 return to the event-date return and subtract the
estimation period mean return.
Tables 6 and 7 report the rejection rates for the NYSE-AMEX and
Nasdaq stocks respectively when the variance increases on the
event date. As expected the Patell test rejects the true null
hypothesis too often when there is a variance increase on the
event date for the NYSE-AMEX and Nasdaq stocks. The rank test
also rejects the true null hypothesis for the lower tail too often
for both samples. At the 1% nominal significance level for Nasdaq
stocks, the rank test also rejects too frequently for the upper
tail tests. The generalized sign rejects the null hypothesis too
often in the upper tail for the Nasdaq sample but only at 5% nominal
significance levels. The standardized cross-sectional test exhibits
correct specification with variance increases.
The results in tables 6 and 7 suggest that the use of Scholes-Williams
betas does not help reduce the excessive rejection problem and
makes no material difference in test statistic performance. Therefore,
further Scholes-Williams beta results are not presented but are
available upon request from the authors.
- Tests on Volume-Clustered Samples with no increase in return
variance
The sampling procedure used above causes stocks with a long trading
history in the Nasdaq market to enter the sample more often, simply
because they have data available on more dates. These stocks may
tend to be the more heavily traded Nasdaq stocks. Moreover, the
range of trading activity for both the NYSE-AMEX and Nasdaq markets
varies significantly, implying a need to segment based on trading
volume. This section presents simulation results using samples
grouped by trading volume.
Table 8 reports upper-tail and lower-tail simulation results at
the 5% nominal significance level for volume based deciles of
NYSE and AMEX stocks; table 9 reports the parallel results for
Nasdaq stocks. Upper-tailed tests using thinly traded NYSE-AMEX
stocks tend to reject the null hypothesis too often with the Patell
test. This result is even stronger for Nasdaq stocks, extending
consistently throughout the lower half of the deciles of upper-tailed
Patell tests and also for many of the lower deciles of lower-tailed
tests. These findings are consistent with misspecification of
the Patell test reported by Campbell and Wasley (1993) for general
Nasdaq samples and by Maynes and Rumsey (1993) for thinly traded
TSE samples. The standardized cross-sectional test rejects the
null hypothesis too often in the more actively traded deciles
for NYSE-AMEX and Nasdaq stocks. No other rejection rates are
statistically larger than expected. In general, the results (and
the results presented in tables 4 and 5) are consistent with misspecification
of lower-tailed standardized cross-sectional tests for more actively
traded stocks and upper-tailed Patell tests for more thinly traded
stocks.
Surprisingly, the power to detect moderate abnormal returns of
0.5% and 1.0% using any of the tests is greater for the most thinly
traded sample (decile 1) than the other lower deciles (and often
than any other decile). Evidently the relative lack of trading
activity in decile 1 makes a moderate abnormal return all the
more conspicuous, given relatively stable market returns.
Table 10 is a comparison of the power of standardized cross-sectional,
rank, and generalized sign tests at induced abnormal returns of
0.5% and 1.0% for the NYSE-AMEX sample by decile. The rank test
is significantly more powerful than the standardized cross-sectional
test for all deciles, and both upper and lower-tailed tests. The
rank test outperforms the generalized sign test for all deciles
of lower-tailed tests, and for upper-tailed tests of more actively
traded deciles at induced abnormal returns of 1.0%. The power
of the generalized sign test is greater for the upper-tail tests
of more thinly traded stocks at a 0.5% induced abnormal return.
Table 11 presents the results for the Nasdaq samples. As with
the NYSE-AMEX samples, the rank test outperforms the standardized
cross-sectional test in all deciles for both upper and lower-tailed
tests. The rank test consistently outperforms the generalized
sign test for the lower-tailed tests of Nasdaq stocks and the
generalized sign test tends to outperform the rank test for the
0.5% induced abnormal returns of upper-tailed tests at mid- to
high-volume deciles.
- Tests on volume-clustered samples with an increase in return
variance
Tables 12 and 13 report the NYSE-AMEX and Nasdaq simulation results
by decile when there is a doubling of the event date return variance.
The standardized test rejects the null hypothesis with no abnormal
return added from 9% to 20% of the time. Clearly, the standardized
test is unacceptable when there is an event-related variance increase.
This conclusion holds regardless of the trading frequency or location
of the stocks.
Against an upper-tailed alternative, the standardized cross-sectional
test does not reject the null hypothesis with no abnormal return
added significantly more than 5% of the time except for NYSE-AMEX
decile 1, where the 6.7% rejection rate still is within the 99%
confidence interval. However, against a lower-tailed alternative,
the standardized cross-sectional test rejects the null more often
than the 99% confidence limit of 6.8% in two NYSE-AMEX and two
Nasdaq samples, both in the upper trading volume deciles.
The rank test lower-tail rejection rate under the null hypothesis
exceeds the 99% confidence limit in every sample except one, where
it is at the limit. This result is consistent with the finding
of Cowan (1992) for general Nasdaq samples. The upper-tail rate
exceeds the limit in 6 of the 7 most thinly traded Nasdaq samples.
The upper-tail rejection frequency is within the 99% confidence
limit for all NYSE-AMEX samples but exceeds the 95% confidence
limit in deciles 1, 3 and 6. Thus, when the return variance increases
on the event date, the rank test is consistently well specified
only for upper tailed tests on actively traded samples.
The generalized sign statistic is well specified or conservative
for all lower-tailed tests. It rejects in favor of an upper-tailed
alternative too frequently in NYSE-AMEX decile 1 at the 99% confidence
level and also in deciles 3 and 6 at the 95% confidence level.
The upper-tailed generalized sign test is well specified only
in the single most actively traded of the Nasdaq deciles.
- Conclusions
The traditional Patell standardized test is poorly specified for
thinly traded stocks, even on the NYSE and AMEX. This conclusion
complements the finding of misspecification by Campbell and Wasley
(1993) and Maynes and Rumsey (1993) for markets where thin trading
is pervasive. The best replacement for the standardized test depends
on the conditions of the study. If the return variance is unlikely
to increase on the event date, the rank test presents the best
specification and power for general use. However, the generalized
sign test also is well specified and offers at least as much power
to detect a small positive abnormal return. Both the rank and
generalized sign tests are much more powerful than the standardized
cross-sectional test in thinly traded samples without sacrificing
power in the actively traded samples. Users of the standardized
cross-sectional test should mind its tendency to reject a true
null hypothesis too often with a lower-tailed alternative in some
samples.
When the return variance increases on the event date, the Patell
test is severely misspecified even for actively traded stocks.
None of the other three tests is an ideal replacement in this
situation. The standardized cross-sectional test is robust to
variance increases for upper-tailed alternatives, but is not very
powerful. With lower-tailed alternatives, it is misspecified in
some volume deciles. If the expected variance increase does not
occur, the standardized cross-sectional test runs a greater risk
of misspecification. The rank statistic is badly misspecified
in lower-tailed tests regardless of volume and in upper-tail tests
for several samples. The generalized sign test is misspecified
in some thinly traded samples when the alternative is upper-tailed
but is conservative with lower-tailed alternatives. Thus, the
standardized cross-sectional statistic should be preferred for
upper-tailed tests and the generalized sign statistic for lower-tailed
tests. The main risk in this prescription is that the researcher
gives up the superior power of the rank statistic if the expected
variance increase does not occur.
Acknowledgments
The authors are grateful to James Larsen, Nandkumar
Nayar, Ajai Singh, David Suk, session participants at the 1995
Financial Management Association meeting and two anonymous referees
of the Journal of Banking and Finance for helpful comments.
References
Atchison, M.D., 1986, Non-representative trading frequencies and
the detection of abnormal performance, Journal of Financial
Research 9, 343-348.
Boehmer, E., J. Musumeci, and A.B. Poulsen, 1991, Event-study
methodology under conditions of event-induced variance, Journal
of Financial Economics 30, 253-272.
Brown, S.J. and J.B. Warner, 1985, Using daily stock returns:
The case of event studies, Journal of Financial Economics
14, 3-31.
Campbell, C.J. and C.E. Wasley, 1993, Measuring security price
performance using daily NASDAQ returns, Journal of Financial
Economics 33, 73-92.
Cohen, K., S. Maier, R. Schwartz and D. Whitcomb, 1986, The microstructure
of securities markets (Prentice-Hall, Engelwood Cliffs).
Corrado, C.J., 1989, A nonparametric test for abnormal security-price
performance in event studies, Journal of Financial Economics
23, 385-395.
Corrado, C.J. and T.L. Zivney, 1992, The specification and power
of the sign test in event study hypothesis tests using daily stock
returns, Journal of Financial and Quantitative Analysis
27(3), 465-478.
Cowan, A.R., 1992, Nonparametric event study tests, Review
of Quantitative Finance and Accounting 2, 343-358.
Dimson, E., 1979, Risk measurement when shares are subject to
infrequent trading, Journal of Financial Economics 7, 197-226.
Dyckman, T., D. Philbrick, and J. Stephan, 1984, A comparison
of event study methodologies using daily stock returns: A simulation
approach, Journal of Accounting Research 22 supplement,
1-30.
Maynes, E. and J. Rumsey, 1993, Conducting event studies with
thinly traded stocks, Journal of Banking and Finance 17,
145-157.
Moore, N.H., D.R. Peterson, and P.P. Peterson, 1986, Shelf registrations
and shareholder wealth: A comparison of shelf and traditional
equity offerings, Journal of Finance 41, 451-463.
Patell, J.M., 1976, Corporate forecasts of earnings per share
and stock price behavior: Empirical tests, Journal of Accounting
Research 14, 246-276.
Peterson, P.P., 1989, Event studies: A review of issues and methodology,
Quarterly Journal of Business and Economics 28(3), 36-66.
Scholes, M. and J.T. Williams, 1977, Estimating betas from nonsynchronous
data, Journal of Financial Economics 5, 309-327.
Table 1
Trading volume decile portfolios for randomly selected stock-event
date combinations.
| Mean Number of Shares Traded for 255 Trading Days
|
| nyse-amex
| | Nasdaq
|
| Decile |
Mean | Minimum
| Maximum | |
Mean | Minimum
| Maximum |
| 1
| 367 | 0
| 654 | |
483 | 0
| 958 |
| 2
| 978 | 654
| 1321 | |
1544 | 958
| 2193 |
| 3
| 1751 | 1321
| 2234 | |
2987 | 2193
| 3857 |
| 4
| 2839 | 2234
| 3534 | |
4928 | 3857
| 6138 |
| 5
| 4450 | 3534
| 5503 | |
7674 | 6138
| 9364 |
| 6 | 6965
| 5504 | 8719
| | 11,553
| 9364 | 14,115
|
| 7 | 11,416
| 8719 | 14,866
| | 17,568
| 14,115 | 21,740
|
| 8 | 20,336
| 14,866 | 27,625
| | 28,063
| 21,741 | 36,091
|
| 9 | 43,768
| 27,626 | 69,809
| | 50,220
| 36,092 | 70,431
|
| 10 |
216,854 | 69,809
| 3,051,747 |
| 192,160 | 70,431
| 3,354,492 |
Table 2
Properties of daily abnormal returns with no abnormal performance
induced based on ordinary least squares betas; randomly selected
stocks and event dates from 1963 (NYSE-AMEX), 1973 (Nasdaq overall)
or 1983 (Nasdaq deciles) through 1993.
| Volume decile
| Average
meana
| Average standard deviation
| Average skewness | Average kurtosis (centered)
| Average studentized range
|
| nyse-amex stocks
|
| Overall
| 0.0000 | 0.0268 | 0.5927
| 4.9948 | 7.9683 |
| 1 | 0.0000
| 0.0258 | 0.7634 | 7.4967
| 8.7613 |
| 2 | 0.0000
| 0.0286 | 0.7682 | 5.8878
| 8.2840 |
| 3 | 0.0000
| 0.0281 | 0.6977 | 5.0439
| 8.0186 |
| 4 | 0.0000
| 0.0282 | 0.6538 | 4.5864
| 7.8789 |
| 5 | 0.0000
| 0.0278 | 0.6316 | 4.5559
| 7.8333 |
| 6 | 0.0000
| 0.0279 | 0.5639 | 3.9839
| 7.7259 |
| 7 | 0.0000
| 0.0275 | 0.5461 | 4.2264
| 7.7566 |
| 8 | 0.0000
| 0.0263 | 0.4760 | 4.3520
| 7.7636 |
| 9 | 0.0000
| 0.0251 | 0.4074 | 4.4469
| 7.7998 |
| 10 |
0.0000 | 0.0228 | 0.3559
| 5.0922 | 7.9044 |
| Nasdaq stocks
|
| Overall
| 0.0000 | 0.0381 | 0.8990
| 12.5676 | 9.3554 |
| 1 | 0.0000
| 0.0293 | 0.6835 | 26.5083
| 10.9501 |
| 2 | 0.0000
| 0.0403 | 0.7202 | 14.5799
| 9.5953 |
| 3 | 0.0000
| 0.0454 | 0.8034 | 11.8192
| 9.0887 |
| 4 | 0.0000
| 0.0468 | 0.8115 | 9.9303
| 8.7747 |
| 5 | 0.0000
| 0.0468 | 0.7972 | 8.6162
| 8.6236 |
| 6 | 0.0000
| 0.0463 | 0.7570 | 7.9599
| 8.5659 |
| 7 | 0.0000
| 0.0465 | 0.7829 | 7.8375
| 8.5768 |
| 8 | 0.0000
| 0.0461 | 0.7273 | 7.0954
| 8.4477 |
| 9 | 0.0000
| 0.0462 | 0.6785 | 7.0817
| 8.4620 |
| 10 |
0.0000 | 0.0459 | 0.5087
| 7.2469 | 8.5807 |
| Upper percentage points for samples of 255 drawn from a normal population
|
| .975 |
- | - | 0.3007 |
0.6013 | 6.59 |
| .995 |
- | - | 0.3951 |
0.7902 | 7.03 |
Table 3
Cross-sectional properties of portfolio abnormal returns on day
0 with no abnormal performance induced; randomly selected stocks
and event dates from 1963 (NYSE-AMEX), 1973 (Nasdaq overall) or
1983 (Nasdaq deciles) through 1993.
| Volume decile
| Mean | Standard deviation
| Skewness | Kurtosis (centered)
| Studentized range |
| NYSE and AMEX stocks
|
| Overall
| 0.0002 | 0.0319 | 0.4727
| 7.1902 | 6.2238 |
| 1 | 0.0006
| 0.0308 | 0.5101 | 7.3203
| 6.3072 |
| 2 | 0.0003
| 0.0330 | 0.5819 | 6.5548
| 6.2062 |
| 3 | 0.0001
| 0.0326 | 0.4680 | 6.6555
| 6.1874 |
| 4 | 0.0002
| 0.0332 | 0.5796 | 6.8712
| 6.1806 |
| 5 | -0.0001
| 0.0324 | 0.4964 | 6.6158
| 6.0842 |
| 6 | 0.0001
| 0.0324 | 0.4982 | 6.6478
| 6.1383 |
| 7 | -0.0001
| 0.0334 | 0.4627 | 8.0324
| 6.3096 |
| 8 | -0.0002
| 0.0312 | 0.4189 | 7.9236
| 6.2764 |
| 9 | -0.0002
| 0.2963 | 0.3087 | 7.3806
| 6.2149 |
| 10 |
-0.0002 | 0.0258 | 0.3550
| 6.5652 | 6.0607 |
| Nasdaq stocks
|
| Overall
| 0.0007 | 0.0458 | 0.5558
| 9.3189 | 6.5911 |
| 1 | 0.0004
| 0.0364 | 0.3721 | 13.1340
| 7.1056 |
| 2 | 0.0007
| 0.0506 | 0.3947 | 10.2514
| 6.6870 |
| 3 | 0.0008
| 0.0573 | 0.4996 | 9.5387
| 6.5889 |
| 4 | 0.0006
| 0.0571 | 0.6090 | 8.4943
| 6.4658 |
| 5 | 0.0002
| 0.0577 | 0.4920 | 8.0535
| 6.4217 |
| 6 | 0.0000
| 0.0560 | 0.4681 | 8.0832
| 6.3800 |
| 7 | -0.0002
| 0.0547 | 0.4117 | 7.9326
| 6.3708 |
| 8 | -0.0000
| 0.0534 | 0.4966 | 7.3775
| 6.2299 |
| 9 | 0.0002
| 0.0529 | 0.5863 | 6.8330
| 6.1990 |
| 10 |
-0.0001 | 0.0539 | 0.4315
| 9.0740 | 6.4535 |
| Upper percentage points for samples of 1000 drawn from a normal population
|
| .975 |
- | - | 0.1518 |
0.3036 | 7.54 |
| .995 |
- | - | 0.1995 |
0.3990 | 7.99 |
Table 4
Rejection rates in 1000 samples of 50 New York and American Stock
Exchange stocks.
| Artificially induced abnormal return
|
| Lower-tailed tests
| Upper-tailed tests
|
| Test | 0.0%
| -0.5% |
-1.0% | -2.0%
| 0.0% |
0.5% | 1.0%
| 2.0% |
| Panel A. 5% significance level
|
| Ordinary least squares betas
|
| Standardized | 4.4%
| 51.0% | 94.6%
| 100.0% | 5.4%
| 51.3% | 94.4%
| 100.0% |
| Standardized cross-sectional
| 6.4% | 53.4%
| 91.4% | 99.7%
| 4.6% | 52.1%
| 95.4% | 100.0%
|
| Rank | 5.5%
| 68.5% | 98.7%
| 100.0% | 5.4%
| 68.7% | 98.8%
| 100.0% |
| Generalized sign | 5.7%
| 57.8% | 93.5%
| 100.0% | 4.1%
| 69.8% | 97.2%
| 100.0% |
| Scholes-Williams betas
|
| Standardized | 5.1%
| 54.1% | 95.4%
| 100.0% | 6.2%
| 53.5% | 95.6%
| 100.0% |
| Standardized cross-sectional
| 6.2% | 53.5%
| 91.6% | 99.7%
| 4.9% | 53.0%
| 95.2% | 100.0%
|
| Rank | 5.6%
| 68.3% | 98.5%
| 100.0% | 5.6%
| 68.2% | 98.8%
| 100.0% |
| Generalized sign | 4.3%
| 56.3% | 93.2%
| 100.0% | 4.4%
| 69.4% | 97.2%
| 100.0% |
| Panel B. 1% significance level
|
| Ordinary least squares betas
| | | |
| | |
| Standardized | 0.6%
| 23.3% | 83.5%
| 100.0% | 0.9%
| 24.5% | 84.1%
| 100.0% |
| Standardized cross-sectional
| 1.6% | 30.1%
| 79.3% | 99.5%
| 0.9% | 25.6%
| 82.9% | 99.9%
|
| Rank | 1.0%
| 41.3% | 92.8%
| 100.0% | 0.8%
| 40.8% | 93.8%
| 100.0% |
| Generalized sign | 0.9%
| 30.3% | 77.5%
| 99.6% | 0.7%
| 43.4% | 90.4%
| 100.0% |
| Scholes-Williams betas
|
| Standardized | 1.0%
| 27.2% | 85.3%
| 100.0% | 1.3%
| 28.2% | 86.2%
| 100.0% |
| Standardized cross-sectional
| 1.5% | 29.8%
| 79.4% | 99.5%
| 0.7% | 25.7%
| 83.0% | 99.9%
|
| Rank | 1.0%
| 41.3% | 92.2%
| 100.0% | 0.7%
| 40.3% | 93.5%
| 100.0% |
| Generalized sign | 1.0%
| 30.0% | 78.1%
| 99.6% | 0.9%
| 43.4% | 90.9%
| 100.0% |
| Panel C. Confidence limits for rejection frequency in 1000 binomial trials
|
| 5% significance level |
| | |
| | | |
|
| 95% confidence interval
| 3.7%-6.4%
| | | |
| | |
| 99% confidence interval
| 3.3%-6.8%
| | | |
| | |
| 1% significance level |
| | |
| | | |
|
| 95% confidence interval
| 0.4%-1.7%
| | | |
| | |
| 99% confidence interval
| 0.3%-1.9%
| | | |
| | |
Table 5
Rejection rates in 1000 samples of 50 Nasdaq stocks.
| Artificially induced abnormal return
|
| Lower-tailed tests
| Upper-tailed tests
|
| Test | 0.0%a
| -0.5% |
-1.0% | -2.0%
| 0.0% |
0.5% | 1.0%
| 2.0% |
| Panel A. 5% significance level
|
| Ordinary least squares betas
|
| Standardized | 5.0%
| 38.8% | 80.8%
| 99.7% | 8.6%
| 41.6% | 86.1%
| 99.9% |
| Standardized cross-sectional
| 5.5% | 39.7%
| 74.7% | 97.2%
| 5.1% | 39.2%
| 83.6% | 99.3%
|
| Rank | 4.1%
| 94.9% | 99.9%
| 100.0% | 6.4%
| 96.0% | 99.7%
| 100.0% |
| Generalized sign | 2.8%
| 77.7% | 95.3%
| 99.6% | 5.5%
| 95.6% | 99.5%
| 100.0% |
| Scholes-Williams betas
|
| Standardized | 5.5%
| 40.4% | 81.4%
| 99.7% | 8.6%
| 42.2% | 86.4%
| 99.9% |
| Standardized cross-sectional
| 5.7% | 39.7%
| 74.5% | 97.2%
| 5.2% | 39.2%
| 83.5% | 99.4%
|
| Rank | 4.8%
| 93.1% | 99.9%
| 100.0% | 7.2%
| 95.1% | 99.6%
| 100.0% |
| Generalized sign | 3.1%
| 76.1% | 94.8%
| 99.9% | 6.1%
| 94.6% | 99.5%
| 100.0% |
| Panel B. 1% significance level
|
| Ordinary least squares betas
| | | |
| | |
| Standardized | 1.0%
| 16.3% | 62.1%
| 98.5% | 3.6%
| 21.3% | 65.4%
| 99.7% |
| Standardized cross-sectional
| 0.9% | 21.4%
| 58.4% | 92.3%
| 1.0% | 16.9%
| 63.0% | 97.6%
|
| Rank | 1.2%
| 84.5% | 98.3%
| 100.0% | 1.0%
| 88.3% | 98.7%
| 100.0% |
| Generalized sign | 0.4%
| 55.7% | 83.2%
| 97.7% | 1.1%
| 87.6% | 98.6%
| 100.0% |
| Scholes-Williams betas
|
| Standardized | 0.9%
| 16.9% | 62.9%
| 98.5% | 3.9%
| 22.2% | 66.5%
| 99.7% |
| Standardized cross-sectional
| 0.7% | 21.5%
| 58.6% | 92.5%
| 1.0% | 16.9%
| 62.9% | 97.8%
|
| Rank | 1.1%
| 81.5% | 98.1%
| 100.0% | 0.7%
| 85.4% | 98.4%
| 100.0% |
| Generalized sign | 0.2%
| 54.3% | 82.6%
| 98.2% | 0.8%
| 84.3% | 98.5%
| 100.0% |
Table 6
Rejection rates when the return variance increases on the event
date in 1000 samples of 50 New York and American Stock Exchange
stocks.
| Artificially induced abnormal return
|
| Lower-tailed tests
| Upper-tailed tests
|
| Test | 0.0%a
| -0.5% |
-1.0% | -2.0%
| 0.0% |
0.5% | 1.0%
| 2.0% |
| Panel A. 5% significance level
|
| Ordinary least squares betas
|
| Standardized | 11.3%
| 48.0% | 86.4%
| 99.9% | 13.2%
| 52.7% | 89.0%
| 100.0% |
| Standardized cross-sectional
| 5.0% | 31.7%
| 70.5% | 98.8%
| 4.1% | 32.7%
| 76.1% | 99.7%
|
| Rank | 10.8%
| 51.9% | 90.3%
| 100.0% | 5.7%
| 45.1% | 87.1%
| 99.9% |
| Generalized sign | 4.3%
| 24.9% | 63.8%
| 97.6% | 6.4%
| 41.0% | 81.5%
| 99.8% |
| Scholes-Williams betas
|
| Standardized | 11.7%
| 50.1% | 87.7%
| 99.9% | 14.4%
| 54.1% | 89.9%
| 100.0% |
| Standardized cross-sectional
| 4.7% | 31.9%
| 70.0% | 98.9%
| 4.0% | 33.5%
| 76.1% | 99.7%
|
| Rank | 10.4%
| 52.4% | 90.0%
| 100.0% | 5.9%
| 44.8% | 86.9%
| 99.9% |
| Generalized sign | 4.3%
| 25.3% | 63.8%
| 97.8% | 6.9%
| 40.6% | 80.4%
| 99.8% |
| Panel B. 1% significance level
|
| Ordinary least squares betas
| | | |
| | |
| Standardized | 4.6%
| 31.0% | 73.1%
| 99.7% | 6.7%
| 34.7% | 76.4%
| 99.8% |
| Standardized cross-sectional
| 1.2% | 14.3%
| 47.5% | 94.9%
| 0.6% | 10.4%
| 50.2% | 97.9%
|
| Rank | 3.1%
| 30.0% | 75.2%
| 100.0% | 1.1%
| 23.0% | 69.6%
| 99.8% |
| Generalized sign | 1.0%
| 8.4% | 34.2%
| 91.1% | 1.0%
| 17.4% | 57.5%
| 98.2% |
| Scholes-Williams betas
|
| Standardized | 5.0%
| 34.2% | 75.0%
| 99.8% | 7.6%
| 37.7% | 78.8%
| 99.8% |
| Standardized cross-sectional
| 1.1% | 14.3%
| 47.6% | 95.0%
| 0.6% | 10.6%
| 49.9% | 98.0%
|
| Rank | 3.1%
| 29.9% | 74.6%
| 100.0% | 1.0%
| 23.1% | 69.4%
| 99.8% |
| Generalized sign | 0.8%
| 8.7% | 35.0%
| 90.8% | 1.2%
| 17.4% | 57.4%
| 98.2% |
Table 7
Rejection rates of one-tailed tests when the return variance increases
on the event date in 1000 samples of 50 Nasdaq Stocks.
| Artificially induced abnormal return
|
| Lower-tailed tests
| Upper tailed tests
|
| Test | 0.0%a
| -0.5% |
-1.0% | -2.0%
| 0.0% |
0.5% | 1.0%
| 2.0% |
| Panel A. 5% significance level
|
| Ordinary least squares betas
|
| Standardized | 11.9%
| 40.3% | 72.6%
| 97.8% | 16.4%
| 46.2% | 78.9%
| 98.9% |
| Standardized cross-sectional
| 5.0% | 22.7%
| 54.6% | 89.9%
| 4.9% | 24.6%
| 61.0% | 96.0%
|
| Rank | 11.6%
| 83.9% | 97.0%
| 100.0% | 6.0%
| 82.5% | 96.2%
| 99.9% |
| Generalized sign | 1.9%
| 40.0% | 74.6%
| 96.1% | 7.7%
| 78.3% | 95.8%
| 99.7% |
| Scholes-Williams betas
|
| Standardized | 11.5%
| 40.4% | 73.4%
| 98.0% | 16.8%
| 47.0% | 79.1%
| 99.0% |
| Standardized cross-sectional
| 5.0% | 22.8%
| 54.2% | 90.3%
| 4.8% | 24.6%
| 61.2% | 96.2%
|
| Rank | 11.0%
| 81.7% | 96.7%
| 100.0% | 6.0%
| 78.9% | 95.8%
| 99.8% |
| Generalized sign | 1.3%
| 41.2% | 74.0%
| 96.5% | 7.5%
| 75.0% | 93.9%
| 99.5% |
| Panel B. 1% significance level
|
| Ordinary least squares betas
| | | |
| | |
| Standardized | 5.1%
| 20.8% | 57.7%
| 95.8% | 8.5%
| 28.5% | 64.2%
| 97.7% |
| Standardized cross-sectional
| 1.0% | 8.9%
| 30.6% | 78.3%
| 1.2% | 8.0%
| 33.3% | 85.1%
|
| Rank | 3.8%
| 66.5% | 90.5%
| 99.4% | 2.1%
| 61.8% | 89.6%
| 99.3% |
| Generalized sign | 0.2%
| 16.4% | 45.3%
| 83.5% | 1.4%
| 53.4% | 85.0%
| 98.2% |
| Scholes-Williams betas
|
| Standardized | 5.2%
| 22.7% | 58.2%
| 96.2% | 9.1%
| 29.2% | 65.3%
| 97.9% |
| Standardized cross-sectional
| 1.0% | 9.2%
| 30.6% | 78.7%
| 1.3% | 7.9%
| 33.4% | 84.8%
|
| Rank | 3.0%
| 63.0% | 89.9%
| 99.5% | 2.3%
| 57.2% | 88.9%
| 99.4% |
| Generalized sign | 0.3%
| 16.1% | 45.8%
| 83.9% | 1.3%
| 49.9% | 82.9%
| 98.2% |
Table 8
Rejection rates in 1000 samples of 50 NYSE-AMEX stocks by volume
decile (1=lowest)
at the 5% significance level.
| Artificially induced abnormal return
|
| Lower-tailed tests
| Upper tailed tests
|
| 0.0%a
| -0.5% | -1.0%
| -2.0% | 0.0%
| 0.5% | 1.0%
| 2.0% |
| Standardized test
| | | |
| | | |
| Decile 1 | 4.5%
| 54.0% | 95.4%
| 100.0% | 9.7%
| 62.6% | 97.2%
| 100.0% |
| Decile 2 | 5.4%
| 47.8% | 92.6%
| 100.0% | 5.2%
| 49.4% | 93.6%
| 100.0% |
| Decile 3 | 3.9%
| 44.6% | 92.7%
| 100.0% | 6.4%
| 51.0% | 95.1%
| 100.0% |
| Decile 4 | 4.1%
| 47.2% | 92.8%
| 99.8% | 5.5%
| 48.1% | 94.6%
| 100.0% |
| Decile 5 | 5.0%
| 49.3% | 93.0%
| 100.0% | 5.8%
| 47.9% | 93.4%
| 100.0% |
| Decile 6 | 3.8%
| 47.8% | 93.0%
| 100.0% | 4.5%
| 47.0% | 94.5%
| 100.0% |
| Decile 7 | 4.8%
| 50.9% | 95.4%
| 100.0% | 3.5%
| 47.8% | 94.2%
| 100.0% |
| Decile 8 | 4.5%
| 55.4% | 95.3%
| 100.0% | 5.4%
| 47.3% | 95.7%
| 100.0% |
| Decile 9 | 5.2%
| 53.8% | 96.6%
| 100.0% | 3.7%
| 49.2% | 95.1%
| 100.0% |
| Decile 10 | 4.6%
| 56.1% | 98.2%
| 100.0% | 3.4%
| 57.4% | 97.7%
| 100.0% |
| Standardized cross-sectional test
| | | |
| | |
| Decile 1 | 5.9%
| 53.6% | 90.5%
| 99.7% | 6.2%
| 62.4% | 96.0%
| 99.9% |
| Decile 2 | 6.3%
| 49.5% | 88.4%
| 99.9% | 4.0%
| 49.9% | 93.0%
| 100.0% |
| Decile 3 | 4.6%
| 47.4% | 89.4%
| 100.0% | 4.1%
| 52.8% | 94.0%
| 100.0% |
| Decile 4 | 5.8%
| 49.5% | 89.5%
| 99.3% | 4.3%
| 49.2% | 94.1%
| 100.0% |
| Decile 5 | 6.7%
| 51.9% | 90.6%
| 99.8% | 4.8%
| 49.9% | 93.4%
| 99.9% |
| Decile 6 | 5.7%
| 51.8% | 91.1%
| 99.8% | 3.7%
| 51.2% | 94.3%
| 99.9% |
| Decile 7 | 7.4%
| 52.8% | 93.3%
| 100.0% | 4.0%
| 51.4% | 94.1%
| 99.9% |
| Decile 8 | 6.4%
| 59.1% | 93.8%
| 100.0% | 4.2%
| 51.5% | 95.6%
| 100.0% |
| Decile 9 | 7.5%
| 58.1% | 96.5%
| 99.9% | 3.8%
| 55.0% | 94.4%
| 100.0% |
| Decile 10 | 6.8%
| 62.4% | 96.9%
| 99.9% | 3.8%
| 62.3% | 97.6%
| 100.0% |
| Rank test |
| | | |
| | | |
| Decile 1 | 5.0%
| 79.1% | 99.3%
| 100.0% | 6.3%
| 82.7% | 99.6%
| 100.0% |
| Decile 2 | 5.3%
| 68.3% | 98.5%
| 100.0% | 4.0%
| 66.7% | 99.1%
| 100.0% |
| Decile 3 | 3.8%
| 64.0% | 98.4%
| 100.0% | 3.9%
| 68.5% | 98.4%
| 100.0% |
| Decile 4 | 4.8%
| 62.4% | 97.8%
| 100.0% | 5.4%
| 63.8% | 98.0%
| 100.0% |
| Decile 5 | 5.3%
| 65.9% | 96.8%
| 100.0% | 5.2%
| 61.2% | 97.5%
| 100.0% |
| Decile 6 | 5.3%
| 62.4% | 97.6%
| 100.0% | 5.5%
| 61.4% | 97.5%
| 100.0% |
| Decile 7 | 6.6%
| 65.1% | 97.7%
| 100.0% | 5.1%
| 62.7% | 98.3%
| 100.0% |
| Decile 8 | 4.9%
| 68.7% | 98.6%
| 100.0% | 4.2%
| 65.6% | 98.6%
| 100.0% |
| Decile 9 | 5.0%
| 69.3% | 98.8%
| 100.0% | 4.2%
| 66.5% | 98.5%
| 100.0% |
| Decile 10 | 5.4%
| 72.9% | 99.6%
| 100.0% | 4.8%
| 72.2% | 99.3%
| 100.0% |
| Generalized sign test
| | | |
| | | |
| Decile 1 | 4.6%
| 71.9% | 96.5%
| 100.0% | 6.1%
| 90.2% | 99.5%
| 100.0% |
| Decile 2 | 5.4%
| 58.6% | 92.6%
| 100.0% | 4.5%
| 74.7% | 98.3%
| 100.0% |
| Decile 3 | 4.7%
| 52.9% | 91.9%
| 100.0% | 3.7%
| 71.0% | 97.5%
| 100.0% |
| Decile 4 | 4.5%
| 53.1% | 90.9%
| 100.0% | 4.7%
| 66.6% | 97.3%
| 100.0% |
| Decile 5 | 5.8%
| 53.8% | 90.5%
| 100.0% | 4.6%
| 62.5% | 96.7%
| 100.0% |
| Decile 6 | 4.3%
| 51.2% | 91.3%
| 100.0% | 4.0%
| 61.8% | 96.2%
| 100.0% |
| Decile 7 | 5.9%
| 53.2% | 91.7%
| 100.0% | 5.4%
| 63.1% | 96.7%
| 100.0% |
| Decile 8 | 5.0%
| 57.2% | 93.8%
| 100.0% | 4.5%
| 65.9% | 97.3%
| 100.0% |
| Decile 9 | 4.6%
| 56.2% | 95.0%
| 100.0% | 3.6%
| 67.3% | 97.3%
| 100.0% |
| Decile 10 | 5.7%
| 59.2% | 96.6%
| 100.0% | 5.5%
| 69.4% | 98.1%
| 100.0% |
Table 9
Rejection rates in 1000 samples of 50 Nasdaq stocks by volume
decile (1=lowest)
at the 5% significance level.
| Artificially induced abnormal return
|
| Lower-tailed tests
| Upper-tailed tests
|
| 0.0%a
| -0.5% | -1.0%
| -2.0% | 0.0%
| 0.5% | 1.0%
| 2.0% |
| Standardized test
| | | |
| | | |
| Decile 1 | 7.5%
| 65.1% | 96.8%
| 99.9% | 9.3%
| 66.7% | 97.3%
| 100.0% |
| Decile 2 | 5.8%
| 32.2% | 75.9%
| 99.1% | 8.2%
| 39.8% | 82.0%
| 99.8% |
| Decile 3 | 6.3%
| 26.7% | 63.5%
| 98.2% | 7.4%
| 33.1% | 69.6%
| 98.9% |
| Decile 4 | 6.4%
| 26.9% | 61.0%
| 96.8% | 6.4%
| 29.1% | 63.1%
| 98.9% |
| Decile 5 | 6.6%
| 28.5% | 62.6%
| 96.4% | 8.0%
| 26.2% | 58.8%
| 97.8% |
| Decile 6 | 6.9%
| 29.6% | 64.2%
| 97.1% | 7.5%
| 24.9% | 57.9%
| 97.9% |
| Decile 7 | 5.4%
| 26.6% | 62.6%
| 97.9% | 5.3%
| 21.5% | 58.5%
| 97.8% |
| Decile 8 | 6.2%
| 25.8% | 60.7%
| 97.8% | 4.8%
| 21.9% | 57.1%
| 97.5% |
| Decile 9 | 5.5%
| 26.7% | 59.4%
| 95.8% | 6.5%
| 22.6% | 55.4%
| 97.2% |
| Decile 10 | 5.7%
| 21.7% | 58.7%
| 97.3% | 4.6%
| 21.6% | 56.0%
| 97.1% |
| Standardized cross-sectional test
| | | |
| | |
| Decile 1 | 4.7%
| 61.7% | 91.8%
| 98.9% | 5.0%
| 63.2% | 93.6%
| 99.0% |
| Decile 2 | 4.7%
| 33.6% | 71.8%
| 96.8% | 4.6%
| 36.9% | 77.1%
| 98.7% |
| Decile 3 | 5.8%
| 24.8% | 59.0%
| 94.8% | 3.7%
| 29.3% | 65.3%
| 96.4% |
| Decile 4 | 6.2%
| 27.8% | 59.2%
| 94.5% | 4.3%
| 24.9% | 60.7%
| 96.7% |
| Decile 5 | 6.9%
| 28.6% | 58.8%
| 92.6% | 4.2%
| 22.2% | 56.8%
| 96.1% |
| Decile 6 | 6.4%
| 29.3% | 61.7%
| 93.5% | 4.5%
| 22.3% | 56.2%
| 96.4% |
| Decile 7 | 6.7%
| 27.8% | 62.5%
| 95.0% | 3.0%
| 21.7% | 58.8%
| 97.0% |
| Decile 8 | 7.4%
| 27.1% | 61.1%
| 94.8% | 2.7%
| 21.0% | 58.2%
| 95.9% |
| Decile 9 | 7.0%
| 29.0% | 59.3%
| 92.8% | 4.1%
| 21.3% | 56.3%
| 96.7% |
| Decile 10 | 6.2%
| 24.5% | 59.3%
| 95.2% | 3.8%
| 22.8% | 58.2%
| 95.5% |
| Rank test |
| | | |
| | | |
| Decile 1 | 4.9%
| 100.0% | 100.0%
| 100.0% | 6.2%
| 100.0% | 100.0%
| 100.0% |
| Decile 2 | 3.4%
| 98.8% | 99.8%
| 100.0% | 5.0%
| 99.5% | 100.0%
| 100.0% |
| Decile 3 | 4.5%
| 95.1% | 99.6%
| 100.0% | 5.9%
| 94.8% | 99.6%
| 100.0% |
| Decile 4 | 5.2%
| 86.1% | 98.0%
| 100.0% | 4.5%
| 83.3% | 97.3%
| 100.0% |
| Decile 5 | 5.2%
| 75.3% | 94.5%
| 99.9% | 6.0%
| 74.2% | 94.8%
| 100.0% |
| Decile 6 | 5.0%
| 71.4% | 94.4%
| 99.8% | 4.4%
| 68.4% | 93.1%
| 99.8% |
| Decile 7 | 5.5%
| 64.9% | 93.2%
| 99.9% | 4.4%
| 63.3% | 92.3%
| 99.9% |
| Decile 8 | 5.6%
| 59.1% | 90.5%
| 99.9% | 3.8%
| 56.4% | 88.3%
| 99.8% |
| Decile 9 | 5.9%
| 52.9% | 87.3%
| 100.0% | 5.5%
| 47.2% | 85.2%
| 99.7% |
| Decile 10 | 6.0%
| 58.5% | 92.3%
| 99.9% | 3.8%
| 60.4% | 91.8%
| 99.9% |
| Generalized sign test
| | | |
| | | |
| Decile 1 | 1.6%
| 99.7% | 99.9%
| 100.0% | 2.6%
| 100.0% | 100.0%
| 100.0% |
| Decile 2 | 2.0%
| 94.1% | 98.6%
| 99.6% | 4.9%
| 99.4% | 100.0%
| 100.0% |
| Decile 3 | 2.4%
| 84.8% | 96.2%
| 99.5% | 5.4%
| 96.0% | 99.2%
| 100.0% |
| Decile 4 | 3.1%
| 74.8% | 91.9%
| 98.8% | 4.3%
| 88.7% | 98.2%
| 100.0% |
| Decile 5 | 4.6%
| 65.3% | 89.7%
| 98.5% | 5.3%
| 83.6% | 97.2%
| 100.0% |
| Decile 6 | 3.1%
| 62.4% | 88.7%
| 98.9% | 5.5%
| 80.0% | 96.0%
| 99.8% |
| Decile 7 | 3.7%
| 58.2% | 85.8%
| 98.7% | 5.1%
| 71.6% | 93.9%
| 99.7% |
| Decile 8 | 4.3%
| 47.4% | 79.3%
| 98.5% | 5.1%
| 68.2% | 92.1%
| 99.9% |
| Decile 9 | 5.2%
| 42.1% | 72.7%
| 98.4% | 5.8%
| 54.5% | 87.9%
| 99.3% |
| Decile 10 | 4.1%
| 42.9% | 78.4%
| 99.0% | 4.2%
| 55.1% | 89.5%
| 99.9% |
Table 10
Difference in rejection rates (and Z statistic for testing difference=0
in parentheses) of rank
versus standardized cross-sectional and generalized sign versus
rank tests; New York
and American stocks by volume decile (1=lowest) at the 5% significance
level.
| Artificially induced abnormal return
|
| Rank v. standardized cross-sectional
| Generalized sign v. rank
|
| Test |
-0.50% | -1.00%
| 0.50% | 1.00%
| -0.50% | -1.00%
| 0.50% | 1.00%
|
| Overall | 15.1%
| 7.3% | 16.6%
| 3.4% | -10.7%
| -5.2% | 1.1%
| -1.6% |
| (6.92)
| (7.53) | (7.59)
| (4.53) | (-4.96)
| (-6.01) | (0.53)
| (-2.56) |
| Decile 1 | 25.5%
| 8.8% | 20.3%
| 3.6% | -7.2%
| -2.8% | 7.5%
| -0.1% |
| (12.07)
| (8.94) | (10.17)
| (5.49) | (-3.74)
| (-4.37) | (4.90)
| (-0.33) |
| Decile 2 | 18.8%
| 10.1% | 16.8%
| 6.1% | -9.7%
| -5.9% | 8.0%
| -0.5% |
| (8.54)
| (9.13) | (7.62)
| (7.00) | (-4.50)
| (-6.40) | (3.93)
| (-1.05) |
| Decile 3 | 14.5%
| 9.0% | 18.8%
| 5.6% | -6.3%
| -6.2% | 3.6%
| -0.4% |
| (6.54)
| (8.41) | (8.55)
| (6.11) | (-2.89)
| (-6.55) | (1.76)
| (-0.67) |
| Decile 4 | 12.9%
| 8.3% | 14.6%
| 3.9% | -9.3%
| -6.9% | 2.8%
| -0.7% |
| (5.81)
| (7.61) | (6.59)
| (4.48) | (-4.21)
| (-6.68) | (1.31)
| (-1.03) |
| Decile 5 | 14.0%
| 6.2% | 11.3%
| 4.1% | -12.1%
| -6.3% | 1.3%
| -0.8% |
| (6.36)
| (5.71) | (5.08)
| (4.40) | (-5.52)
| (-5.78) | (0.60)
| (-1.07) |
| Decile 6 | 10.6%
| 6.5% | 10.2%
| 3.2% | -11.2%
| -6.3% | 0.4%
| -1.3% |
| (4.79)
| (6.30) | (4.60)
| (3.61) | (-5.06)
| (-6.15) | (0.18)
| (-1.66) |
| Decile 7 | 12.3%
| 4.4% | 11.3%
| 4.2% | -11.9%
| -6.0% | 0.4%
| -1.6% |
| (5.59)
| (4.75) | (5.10)
| (4.91) | (-5.41)
| (-5.99) | (0.19)
| (-2.29) |
| Decile 8 | 9.6%
| 4.8% | 14.1%
| 3.0% | -11.5%
| -4.8% | 0.3%
| -1.3% |
| (4.47)
| (5.61) | (6.40)
| (4.00) | (-5.32)
| (-5.61) | (0.14)
| (-2.05) |
| Decile 9 | 11.2%
| 2.3% | 11.6%
| 4.1% | -13.1%
| -3.8% | 0.7%
| -1.2% |
| (5.21)
| (3.40) | (5.31)
| (4.95) | (-6.06)
| (-4.90) | (0.33)
| (-1.87) |
| Decile 10 | 10.5%
| 2.7% | 10.0%
| 1.7% | -13.7%
| -3.0% | -2.9%
| -1.2% |
| (5.02)
| (4.60) | (4.77)
| (3.08) | (-6.47)
| (-4.91) | (-1.43)
| (-2.37) |
Table 11
Difference in rejection rates (and Z statistic for testing difference=0
in parentheses) of rank
versus standardized cross-sectional and generalized sign versus
rank tests;
Nasdaq stocks by volume decile (1=lowest) at the 5% significance
level.
| Artificially induced abnormal return
|
| Rank v. standardized cross-sectional
| Generalized sign v. rank
|
| Test |
-0.50% | -1.00%
| 0.50% | 1.00%
| -0.50% | -1.00%
| 0.50% | 1.00%
|
| Overall | 55.2%
| 25.2% | 56.8%
| 16.1% | -17.2%
| -4.6% | -0.40%
| -0.20% |
| (26.31)
| (16.92) | (27.14)
| (13.01) | (-11.19)
| (-6.72) | (-0.45)
| (-0.71) |
| Decile 1 | 38.3%
| 8.2% | 36.8%
| 6.4% | -0.3%
| -0.1% | 0.00%
| 0.00% |
| (21.77)
| (9.25) | (21.24)
| (8.13) | (-1.73)
| (-1.00) | -
| - |
| Decile 2 | 65.2%
| 28.0% | 62.6%
| 22.9% | -4.7%
| -1.2% | -0.10%
| 0.00% |
| (30.82)
| (17.94) | (30.06)
| (16.08) | (-5.68)
| (-3.01) | (-0.30)
| - |
| Decile 3 | 70.3%
| 40.6% | 65.5%
| 34.3% | -10.3%
| -3.4% | 1.20%
| -0.40% |
| (32.08)
| (22.41) | (30.18)
| (20.16) | (-7.66)
| (-5.30) | (1.28)
| (-1.16) |
| Decile 4 | 58.3%
| 38.8% | 58.4%
| 36.6% | -11.3%
| -6.1% | 5.40%
| 0.90% |
| (26.33)
| (21.15) | (26.21)
| (20.09) | (-6.37)
| (-6.23) | (3.48)
| (1.36) |
| Decile 5 | 46.7%
| 35.7% | 52.0%
| 38.0% | -10.0%
| -4.8% | 9.40%
| 2.40% |
| (20.90)
| (18.87) | (23.27)
| (19.84) | (-4.89)
| (-3.98) | (5.15)
| (2.74) |
| Decile 6 | 42.1%
| 32.7% | 46.1%
| 36.9% | -9.0%
| -5.7% | 11.60%
| 2.90% |
| (18.83)
| (17.67) | (20.71)
| (18.97) | (-4.28)
| (-4.58) | (5.93)
| (2.86) |
| Decile 7 | 37.1%
| 30.7% | 41.6%
| 33.5% | -6.7%
| -7.4% | 8.30%
| 1.60% |
| (16.64)
| (16.53) | (18.82)
| (17.43) | (-3.08)
| (-5.40) | (3.96)
| (1.41) |
| Decile 8 | 32.0%
| 29.4% | 35.4%
| 30.1% | -11.7%
| -11.2% | 11.80%
| 3.80% |
| (14.45)
| (15.35) | (16.25)
| (15.20) | (-5.24)
| (-6.99) | (5.44)
| (2.86) |
| Decile 9 | 23.9%
| 28.0% | 25.9%
| 28.9% | -10.8%
| -14.6% | 7.30%
| 2.70% |
| (10.87)
| (14.15) | (12.20)
| (14.21) | (-4.84)
| (-8.16) | (3.27)
| (1.77) |
| Decile 10 | 34.0%
| 33.0% | 37.6%
| 33.6% | -15.6%
| -13.9% | -5.30%
| -2.30% |
| (15.43)
| (17.23) | (17.06)
| (17.35) | (-6.98)
| (-8.79) | (-2.40)
| (-1.77) |
Table 12
Rejection rates in 1000 samples of 50 NYSE-AMEX stocks by volume
decile (1=lowest)
at the 5% significance level when the return variance doubles
on the event date.
| Absolute value of artificially induced abnormal return
|
| Lower-tailed tests
| Upper-tailed tests
|
| 0.0%a
| 0.5% | 1.0%
| 2.0% | 0.0%
| 0.5% | 1.0%
| 2.0% |
| Standardized test
| | | |
| | | |
| Decile 1 | 11.2%
| 48.4% | 84.6%
| 100.0% | 19.1%
| 59.4% | 92.4%
| 100.0% |
| Decile 2 | 10.8%
| 44.8% | 84.5%
| 99.9% | 13.8%
| 53.0% | 87.8%
| 99.8% |
| Decile 3 | 12.2%
| 47.1% | 85.1%
| 99.8% | 14.7%
| 51.2% | 86.0%
| 100.0% |
| Decile 4 | 12.7%
| 48.4% | 85.6%
| 99.6% | 12.3%
| 48.7% | 85.8%
| 100.0% |
| Decile 5 | 13.6%
| 50.6% | 87.3%
| 99.8% | 10.7%
| 47.8% | 85.1%
| 99.8% |
| Decile 6 | 12.4%
| 50.2% | 84.5%
| 100.0% | 12.5%
| 47.9% | 85.9%
| 99.6% |
| Decile 7 | 13.3%
| 53.8% | 89.3%
| 100.0% | 10.2%
| 45.9% | 86.2%
| 100.0% |
| Decile 8 | 13.5%
| 55.4% | 90.4%
| 100.0% | 10.1%
| 46.6% | 87.7%
| 100.0% |
| Decile 9 | 14.3%
| 55.5% | 91.4%
| 100.0% | 9.0%
| 47.0% | 87.1%
| 99.9% |
| Decile 10 | 11.7%
| 57.5% | 93.9%
| 100.0% | 9.2%
| 52.0% | 92.0%
| 100.0% |
| Standardized cross-sectional test
| | | |
| | |
| Decile 1 | 4.6%
| 32.2% | 69.8%
| 98.5% | 6.7%
| 38.9% | 82.5%
| 99.6% |
| Decile 2 | 4.7%
| 27.5% | 67.9%
| 97.9% | 4.3%
| 32.4% | 75.7%
| 99.6% |
| Decile 3 | 5.9%
| 30.8% | 70.4%
| 98.5% | 4.6%
| 31.3% | 74.1%
| 99.6% |
| Decile 4 | 5.7%
| 30.8% | 69.1%
| 97.9% | 4.8%
| 30.9% | 70.3%
| 99.7% |
| Decile 5 | 6.5%
| 35.0% | 70.5%
| 98.8% | 3.9%
| 27.8% | 71.5%
| 99.2% |
| Decile 6 | 5.6%
| 32.4% | 72.4%
| 98.2% | 5.1%
| 30.2% | 72.4%
| 99.1% |
| Decile 7 | 7.1%
| 36.3% | 75.3%
| 99.4% | 3.3%
| 28.5% | 72.4%
| 99.3% |
| Decile 8 | 5.2%
| 38.9% | 78.8%
| 99.0% | 4.0%
| 30.1% | 73.8%
| 99.6% |
| Decile 9 | 7.1%
| 39.0% | 80.6%
| 99.5% | 2.5%
| 28.9% | 74.8%
| 99.4% |
| Decile 10 | 6.5%
| 42.3% | 83.8%
| 99.8% | 3.9%
| 35.2% | 81.8%
| 99.9% |
| Rank test |
| | | |
| | | |
| Decile 1 | 9.3%
| 60.7% | 93.4%
| 100.0% | 7.4%
| 58.8% | 93.5%
| 100.0% |
| Decile 2 | 9.1%
| 51.1% | 90.4%
| 100.0% | 4.8%
| 44.9% | 87.5%
| 99.9% |
| Decile 3 | 12.3%
| 53.1% | 88.3%
| 100.0% | 6.6%
| 42.6% | 84.4%
| 100.0% |
| Decile 4 | 10.8%
| 53.8% | 90.0%
| 99.7% | 5.2%
| 40.3% | 82.3%
| 100.0% |
| Decile 5 | 11.0%
| 54.3% | 90.0%
| 100.0% | 3.7%
| 38.8% | 82.7%
| 99.8% |
| Decile 6 | 11.3%
| 51.1% | 88.1%
| 100.0% | 6.7%
| 40.5% | 81.5%
| 99.8% |
| Decile 7 | 12.2%
| 55.1% | 90.1%
| 100.0% | 4.9%
| 38.5% | 84.0%
| 99.9% |
| Decile 8 | 11.0%
| 54.4% | 91.6%
| 100.0% | 5.2%
| 41.8% | 86.7%
| 100.0% |
| Decile 9 | 11.9%
| 58.2% | 95.0%
| 100.0% | 3.5%
| 42.1% | 85.2%
| 100.0% |
| Decile 10 | 10.8%
| 59.3% | 94.1%
| 100.0% | 5.6%
| 48.9% | 91.3%
| 100.0% |
| Generalized sign test
| | | |
| | | |
| Decile 1 | 3.3%
| 33.6% | 71.1%
| 98.8% | 7.3%
| 59.7% | 90.4%
| 99.9% |
| Decile 2 | 3.1%
| 25.3% | 62.6%
| 97.4% | 5.7%
| 43.1% | 82.0%
| 99.5% |
| Decile 3 | 3.8%
| 27.4% | 63.5%
| 96.3% | 6.7%
| 42.3% | 80.0%
| 99.5% |
| Decile 4 | 3.2%
| 26.1% | 62.7%
| 97.4% | 5.7%
| 38.4% | 78.2%
| 99.2% |
| Decile 5 | 4.1%
| 27.1% | 64.4%
| 98.0% | 4.3%
| 35.9% | 75.9%
| 99.6% |
| Decile 6 | 3.4%
| 24.6% | 62.5%
| 97.2% | 6.5%
| 37.4% | 74.7%
| 99.5% |
| Decile 7 | 4.4%
| 27.9% | 64.8%
| 97.7% | 5.8%
| 37.5% | 78.3%
| 99.6% |
| Decile 8 | 3.6%
| 25.0% | 66.5%
| 99.3% | 5.6%
| 39.9% | 80.9%
| 99.9% |
| Decile 9 | 3.5%
| 28.1% | 71.6%
| 99.2% | 3.8%
| 38.0% | 79.1%
| 100.0% |
| Decile 10 | 3.9%
| 30.1% | 71.6%
| 99.4% | 5.1%
| 42.2% | 83.9%
| 99.7% |
Table 13
Rejection rates in 1000 samples of 50 Nasdaq stocks by volume
decile (1=lowest)
at the 5% significance level when the return variance doubles
on the event date.
| Absolute value of artificially induced abnormal return
|
| Lower-tailed tests
| Upper tailed tests
|
| 0.0%a
| 0.5% | 1.0%
| 2.0% | 0.0%
| 0.5% | 1.0%
| 2.0% |
| Standardized test
| | | |
| | | |
| Decile 1 | 15.2%
| 57.1% | 89.4%
| 99.6% | 19.6%
| 64.0% | 93.7%
| 100.0% |
| Decile 2 | 13.5%
| 37.0% | 66.1%
| 96.0% | 18.0%
| 45.1% | 73.1%
| 97.7% |
| Decile 3 | 12.6%
| 32.7% | 59.1%
| 92.8% | 16.4%
| 38.6% | 64.5%
| 94.4% |
| Decile 4 | 13.2%
| 33.6% | 61.3%
| 91.8% | 14.2%
| 31.7% | 57.9%
| 93.9% |
| Decile 5 | 15.0%
| 32.2% | 58.5%
| 91.7% | 14.7%
| 33.3% | 57.8%
| 91.9% |
| Decile 6 | 16.3%
| 37.4% | 61.1%
| 92.7% | 12.5%
| 29.8% | 54.5%
| 91.7% |
| Decile 7 | 15.6%
| 35.8% | 60.0%
| 92.5% | 12.1%
| 31.2% | 53.6%
| 92.3% |
| Decile 8 | 16.2%
| 35.7% | 62.8%
| 92.5% | 10.8%
| 26.9% | 50.2%
| 91.4% |
| Decile 9 | 16.3%
| 34.4% | 58.0%
| 92.1% | 12.8%
| 29.1% | 52.7%
| 89.1% |
| Decile 10 | 15.7%
| 34.8% | 59.6%
| 93.7% | 8.6%
| 25.6% | 48.1%
| 88.7% |
| Standardized cross-sectional test
| | | |
| | |
| Decile 1 | 4.2%
| 37.1% | 74.5%
| 96.4% | 5.9%
| 41.4% | 81.6%
| 98.2% |
| Decile 2 | 5.8%
| 22.9% | 47.7%
| 86.4% | 5.3%
| 22.5% | 53.7%
| 92.5% |
| Decile 3 | 4.7%
| 17.1% | 37.5%
| 78.7% | 4.6%
| 16.1% | 41.5%
| 83.7% |
| Decile 4 | 4.9%
| 17.1% | 39.3%
| 79.7% | 4.8%
| 14.4% | 35.0%
| 80.8% |
| Decile 5 | 6.8%
| 17.3% | 36.5%
| 77.0% | 4.7%
| 15.3% | 35.1%
| 79.9% |
| Decile 6 | 7.1%
| 20.4% | 41.4%
| 80.7% | 4.2%
| 12.7% | 34.1%
| 77.9% |
| Decile 7 | 6.3%
| 20.2% | 42.5%
| 80.5% | 3.3%
| 13.1% | 35.0%
| 78.3% |
| Decile 8 | 6.7%
| 20.8% | 43.1%
| 81.4% | 4.4%
| 12.3% | 31.3%
| 77.8% |
| Decile 9 | 8.2%
| 20.1% | 40.3%
| 80.1% | 3.8%
| 12.0% | 33.4%
| 78.3% |
| Decile 10 | 6.3%
| 19.3% | 41.2%
| 83.2% | 2.9%
| 10.6% | 30.4%
| 75.5% |
| Rank test |
| | | |
| | | |
| Decile 1 | 12.3%
| 99.9% | 100.0%
| 100.0% | 8.5%
| 99.9% | 100.0%
| 100.0% |
| Decile 2 | 7.6%
| 89.8% | 98.3%
| 99.9% | 11.9%
| 90.5% | 97.7%
| 99.9% |
| Decile 3 | 6.8%
| 77.0% | 95.8%
| 99.6% | 10.7%
| 75.1% | 92.2%
| 99.3% |
| Decile 4 | 10.3%
| 63.7% | 87.5%
| 99.2% | 8.8%
| 55.1% | 80.6%
| 98.0% |
| Decile 5 | 11.1%
| 54.6% | 81.6%
| 97.8% | 7.2%
| 45.1% | 72.5%
| 98.0% |
| Decile 6 | 11.2%
| 55.0% | 82.7%
| 99.0% | 6.2%
| 38.9% | 68.7%
| 96.5% |
| Decile 7 | 11.5%
| 51.3% | 79.1%
| 97.8% | 7.2%
| 34.0% | 66.0%
| 94.7% |
| Decile 8 | 12.5%
| 49.8% | 77.6%
| 97.6% | 5.4%
| 28.4% | 58.8%
| 95.0% |
| Decile 9 | 14.0%
| 45.1% | 71.6%
| 97.1% | 5.8%
| 28.2% | 58.2%
| 94.1% |
| Decile 10 | 14.5%
| 52.8% | 80.2%
| 98.4% | 4.1%
| 33.3% | 64.8%
| 96.2% |
| Generalized sign test
| | | |
| | | |
| Decile 1 | 0.8%
| 86.4% | 97.1%
| 99.5% | 8.3%
| 99.7% | 100.0%
| 100.0% |
| Decile 2 | 0.9%
| 50.4% | 83.4%
| 96.0% | 10.1%
| 83.1% | 96.5%
| 99.6% |
| Decile 3 | 1.3%
| 35.3% | 72.8%
| 94.1% | 7.6%
| 65.9% | 89.0%
| 98.6% |
| Decile 4 | 1.4%
| 28.2% | 61.1%
| 89.7% | 9.1%
| 54.7% | 79.7%
| 96.7% |
| Decile 5 | 3.0%
| 25.0% | 52.4%
| 85.8% | 7.9%
| 46.6% | 72.5%
| 96.2% |
| Decile 6 | 2.5%
| 24.1% | 54.1%
| 88.0% | 7.0%
| 39.6% | 68.5%
| 94.7% |
| Decile 7 | 4.0%
| 21.8% | 50.7%
| 84.2% | 7.3%
| 35.5% | 63.0%
| 92.8% |
| Decile 8 | 3.1%
| 19.9% | 46.5%
| 81.4% | 7.3%
| 31.6% | 61.9%
| 93.0% |
| Decile 9 | 3.7%
| 18.0% | 41.9%
| 81.0% | 6.6%
| 29.3% | 56.9%
| 92.1% |
| Decile 10 | 3.9%
| 21.0% | 46.5%
| 83.1% | 5.2%
| 29.3% | 60.9%
| 93.0% |
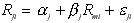 , where
, where 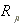 is the rate of return of the
is the rate of return of the 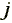 th stock
on day
th stock
on day 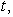 and
and 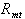 is
the rate of return of the CRSP NYSE-AMEX equally weighted market
index on day
is
the rate of return of the CRSP NYSE-AMEX equally weighted market
index on day 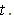 The random noise term
The random noise term 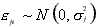 for
for 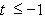 and
and 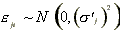 for
for
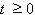 is assumed not to be autocorrelated.
The period for the estimation of the market model parameters is
days -255 through -1, where day 0 is the randomly selected event
date. Initially we assume that
is assumed not to be autocorrelated.
The period for the estimation of the market model parameters is
days -255 through -1, where day 0 is the randomly selected event
date. Initially we assume that 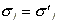 . Although
beta estimation is not the primary focus of the study, betas are
computed using both OLS and the Scholes and Williams (1977) procedure
that adjusts for the effect of thin trading on the market index.
The computation of Scholes-Williams betas requires additional
simple linear regressions of
. Although
beta estimation is not the primary focus of the study, betas are
computed using both OLS and the Scholes and Williams (1977) procedure
that adjusts for the effect of thin trading on the market index.
The computation of Scholes-Williams betas requires additional
simple linear regressions of  on lagged
and leading values of
on lagged
and leading values of 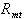 and the estimation
of the first-order autocorrelation of
and the estimation
of the first-order autocorrelation of 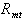 .
.
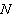
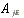
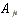
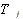
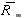

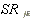

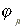
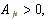 =0 otherwise
=0 otherwise
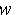
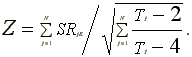
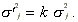 Boehmer, Musumeci and Poulsen
(1991) write the test statistic as
Boehmer, Musumeci and Poulsen
(1991) write the test statistic as
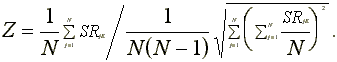
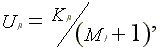
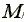 is the number of non-missing abnormal
returns for stock j. The rank test statistic is
is the number of non-missing abnormal
returns for stock j. The rank test statistic is
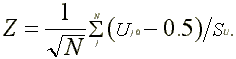
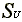 is
is