Abstract: We investigate the effect of non-binding pre-play communication in experiments with simple two-player coordination games. We reproduce the results of other studies in which play converges to a Pareto-dominated equilibrium in the absence of communication, and communication moves outcomes in the direction of the Pareto-dominant equilibrium. However, we provide new results which show that the effectiveness of communication is sensitive to the structure of payoffs. Our results support an argument put forward by Aumann: agreements to play a Nash equilibrium are fragile when players have a strict preference over their opponent's strategy choice. We also find that informative communication does not necessarily lead to the Pareto-dominant equilibrium.

1 Introduction

In this paper we present experimental results on the effect of communication in coordination games, focusing on Aumann's (1990) conjecture that the effect will be sensitive to the structure of payoffs. This conjecture raises questions about whether communication facilitates coordination on Pareto-dominant equilibria, and whether non-binding agreements to play such equilibria are self-enforcing. The notion that players will keep agreements to play Pareto-superior equilibria also underlies the appeal of other selection criteria, such as Coalition-Proofness (Bernheim, Peleg and Whinston, 1987) or Communication-Proofness (Ferreira, 1996).

We investigate Aumann's conjecture using simple two-player coordination games, although it is relevant to a broader class of games (for example see Roth, 1980, and Aumann, 1985). Coordination games have attracted considerable attention among both theorists and empiricists since not only do they exhibit multiple equilibria but they also represent the essential features of many economic models. In these games there are multiple Pareto-rankable Nash equilibria, and so "coordination failures" - failures to achieve the efficient equilibrium - are possible, at a theoretical level, based on Nash's (1951) solution concept. Moreover, coordination failures are observed, at an experimental level (see Cooper et al., 1990, Straub, 1995, or Van Huyck et al., 1990).

It is widely thought that communication will have an important effect on the outcome of these games, and will lead players to Pareto-dominant equilibria (see the discussion in Rasmussen, 1994, for example). Unfortunately, while some may expect, on intuitive grounds, that communication will mitigate coordination failures, the introduction of communication does not, by itself, eliminate any Nash equilibria, and so coordination failures are still possible according to this solution concept.

Aumann (1990) argues that the effectiveness of communication in reducing coordination failures depends crucially on the payoff structure of the game. In his view, communication cannot affect the outcome of the game if, as is the case in some coordination games, each player has a strict preference over the other's strategy choice. In such a case, a player always wants his or her opponent to choose a particular strategy regardless of what they themselves intend to choose, and so, Aumann argues, messages convey no information about what players intend to do, only about what they want their opponents to do. This information, of course, is already common knowledge to the players, and so communication cannot affect the outcome of the game.

Farrell (1988) agrees that Aumann's argument is "compelling" if one thinks of players deciding their move, and then their message. If, on the other hand, players are viewed as deciding on their move after their message, Farrell finds "matters are rather unclear". He offers an alternative intuition for why communication may be effective and enable players to attain the Pareto-dominant equilibrium payoffs. More recently, Farrell and Rabin (1996) acknowledge Aumann's argument, but nevertheless suspect that communication will have some effect in the class of games where the argument applies.

Experimental evidence on the effect of communication in coordination games is limited. Cooper et al. (1990) study a coordination game in which subjects predominantly coordinate on a Pareto-dominated equilibrium in the absence of communication; the risk-dominant properties of this equilibrium appear to overwhelm other considerations. They find that when non-binding pre-play communication is introduced subjects predominantly coordinate on the Pareto-dominant equilibrium. Thus communication is effective in reducing coordination failures. In this game, however, there is a safe strategy and a player intending to play this strategy has no strict preference over his or her opponent's choice, thus Aumann's argument does not apply.

In our experimental games, we reproduce the experimental findings of Cooper et al., and build on them with new and replicable results pertaining to Aumann's conjecture. We go on to study other games which also result in coordination failures in the absence of communication. The main interest in these games is that they allow a careful evaluation of Aumann's argument. We find that when players have a strict preference over opponents' choices, communication has some effect on outcomes, but it is considerably muted. Moreover, in this case we also find that agreements to play a Nash equilibrium are broken more often than not. This shows that the effect of communication is sensitive to small changes in the payoffs of the underlying game, and at the same time supports Aumann's explanation for why this is so. We also find that when communication is effective, it does not always work in the way one might, intuitively, expect.

The rest of the paper is organized as follows. In section 2 we explain the structure of the games, describe how we introduce communication, and review relevant theoretical issues and experimental results. Our experimental design and procedures are outlined in section 3 and the results are presented in section 4. Section 5 concludes.

2 Coordination Games and Communication

There are many situations in which people can benefit from coordinating their decisions, but can coordinate their decisions in different ways. Sometimes, the benefits from coordination depend on which particular coordinated decision is taken. Figure 1 displays the payoff matrix for Game I, an example of a simple two-player coordination game.

----- Figure 1 about here -----

In this Game there are multiple Nash equilibria. According to Harsanyi and Selten (1988) rational players will select (Red, Red) on the basis that it is Pareto dominant, that is, it yields a higher payoff to every player than any other equilibrium. However, there is a sense in which playing Red is "risky," and this may make the safer, but Pareto-dominated, (Blue, Blue) equilibrium more attractive. This is also formalized by Harsanyi and Selten who introduce the concept of risk-dominance. In Game I (Blue, Blue) is a risk-dominant equilibrium.

In experiments with Game I, Cooper et al. (1990) and Straub (1995) report significant occurrences of coordination failures: subjects predominantly play Blue. Van Huyck et al. (1990) also find coordination failures in a more complex game where the Pareto-dominant equilibrium is risky. These results bolster Harsanyi's (1995) contention that one should not simply assume Pareto-dominance as a refinement criterion.

Pareto-dominance may be more appealing if players are allowed to communicate before making their choices. Although the introduction of non-binding pre-play communication does not eliminate any equilibria (it is still an equilibrium for players to 'babble' and ignore messages), it may make the Pareto-dominant equilibrium more likely to emerge. The intuition is that players would agree to play the strategies that form the Pareto-dominant equilibrium, and because these form an equilibrium, this agreement would be self-enforcing.

In Game I, for example, suppose players choose Blue because they are worried their opponent may choose Blue. With communication, players have an opportunity to reassure each other that they recognize the appeal of choosing Red, and intend to play it. We might expect that players would agree to play Red, and play accordingly. In fact, Cooper et al. (1992) find empirical support for this. Using a two-way communication treatment, in which subjects simultaneously announce their intentions prior to making their choices, almost all subjects coordinate on the Pareto-dominant equilibrium in Game I.

Aumann (1990) challenges the idea that communication generally induces efficiency. In some games, he argues, communication will be ineffective because messages are uninformative. Consider Game II, where as before (Red, Red) is Pareto-dominant, (Blue, Blue) is risk-dominant, but now each player has a strict preference over his or her opponent's action. That is, Player I would like Player II to play Red, regardless of his or her own intentions. If the message "I intend to play Red" increases the likelihood of Player II choosing Red, then Player I has an incentive to send this message, even if he really intends to play Blue. Thus, an announcement such as "I intend to play Red" could be sensibly interpreted as coming either from a player planning to play Blue or a player planning to play Red. Player II might then infer "He would say that anyway," and ignore the announcement.

----- Figure 2 about here -----

In their discussion of Game II, Farrell and Rabin (1996) refer to Player I as Artemis, Player II as Calliope, the action Red as "Hunt Stag", and the action Blue as "Hunt Rabbits." They conclude "although we see the force of Aumann's argument, we suspect that cheap talk will do a good deal to bring Artemis and Calliope to the stag hunt." (p.114)

Our contribution in this paper is to bring to bear experimental evidence on how subjects play Games I and II, with and without pre-play communication. Based on previous studies, we expect Game I will result in predominantly Blue play, and communication will induce predominantly Red play. We are unaware of any experiments with Game II prior to ours, but we expect the small payoff differences between Games will have little effect in the absence of communication. Preceding Game II with a round

of communication provides a sharp test of Aumann's conjecture.

3 The Experiment

The experiment was conducted at the University of Manchester using 160 subjects, each of whom participated in one of eight sessions. The first set of four sessions was conducted in Autumn semester, 1994. Another set of four sessions was conducted in Spring semester, 1996, in order to assess the replicability of the results.

Each set of four sessions involved one session using the payoffs from Game I with no pre-play communication, one session using the payoffs from Game II with no pre-play communication, one session using the payoffs from Game I and including pre-play communication, and one session using the payoffs from Game II and including pre-play communication.

The purpose of the sessions without pre-play communication was threefold. First, the comparison of behavior in Games I and II allows investigation of the robustness of behavior to payoff variation per se. Second, these sessions allow us to validate our procedures by comparing our results with those in the existing literature. Most importantly in terms of our focus on Aumann's conjecture, these sessions provide a baseline against which the effect of communication can be judged.

All sessions used the following general procedures. Upon arrival subjects were randomly seated at computer terminals in two connecting rooms. When 10 subjects were seated in each room the session began. Subjects were given a set of written instructions, which monitors then read aloud in both rooms. After hearing the instructions subjects were allowed to ask questions, and then were given a quiz. All subjects completed the quiz correctly, and then the decision-making part of the experiment began. During the session the only permitted communication between subjects was via formal decisions transmitted by pressing keys on a computer terminal. Simultaneous decision making was achieved by transmitting subjects' decisions to the appropriate opponent only after all subjects in both rooms had made their decision.

As in other experiments with coordination games, our sessions had a multi-round design where subjects gained experience of the rules of the game and the payoff implications of their actions by playing repeatedly. Specifically, each session consisted of ten rounds, in each of which subjects took part in the play of a single Game against a different opponent.

The sessions with pre-play communication used identical procedures except that each round consisted of two stages: in the first stage subjects filled in the blank in the sentence "I INTEND TO CHOOSE ", in the second stage they chose their action. It was clearly stated in the instructions: "You are not required to make the choice announced earlier." This is the two-way communication treatment used by Cooper et al. (1990); it has the advantage that in all sessions, each subject has an identical role, and can be given identical instructions.

In each round subjects accumulated points according to their decision and the decision of their opponent. These earnings were added to an initial balance of 4200 points. At the end of the session, each subject received £1 for every 1400 points. The initial balance ensured that subjects earned at least £3 in all sessions. Minimum and maximum earnings were £3.71 and £10.14, and average earnings were £8.20. All sessions were completed in less than an hour. Average earnings for part-time bar work in Manchester were around £4 per hour at this time, so we are satisfied that the rewards available to the subjects were sufficiently high to motivate them to take the experiment seriously.

4 Experimental Results

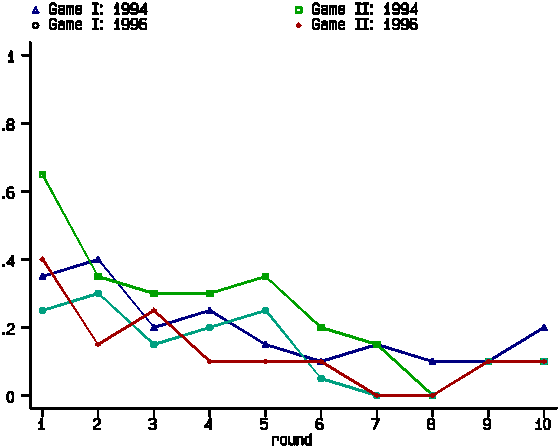
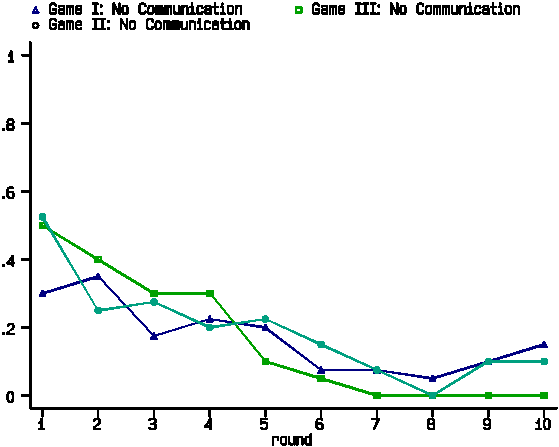
We first describe the results from sessions without communication. Figure 3 displays the proportions of Red choices across rounds in these sessions. The results from all of these sessions are similar to one another: subjects tend to settle on the risk-dominant strategy. This reproduces the essential qualitative features of Cooper et al. (1992) and Straub (1995) for the case of Game I. Further, the small difference in payoffs between Games I and II does not appear to have a significant effect on behavior.

----- Figure 3 about here -----

For formal comparisons between any two sessions we test whether the proportions of Red choices in the final round are the same using Fisher's exact test against a two-sided alternative. To assess the replicability of our results, we compare sessions using the same payoff matrix. For both Game I (observed significance level, p=0.661) and Game II (p=1.000) we accept the null hypothesis of equal proportions of Red choices. After pooling the data from replicate sessions, we find the difference between Games to be statistically insignificant (p=0.737). We conclude that behavior in the 1994 and 1996 sessions of the same Game is essentially the same, and that the attraction of the risk-dominant strategy is not affected by the small parameter differences between Games I and II.

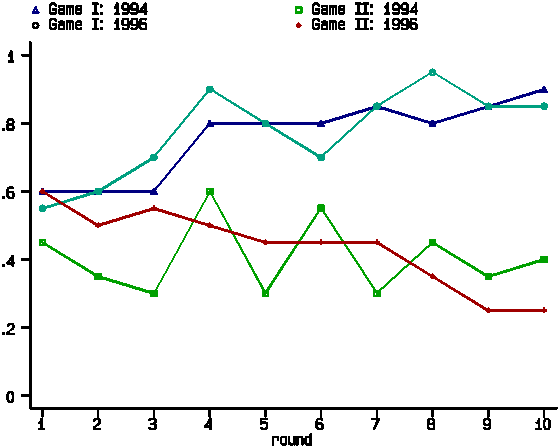
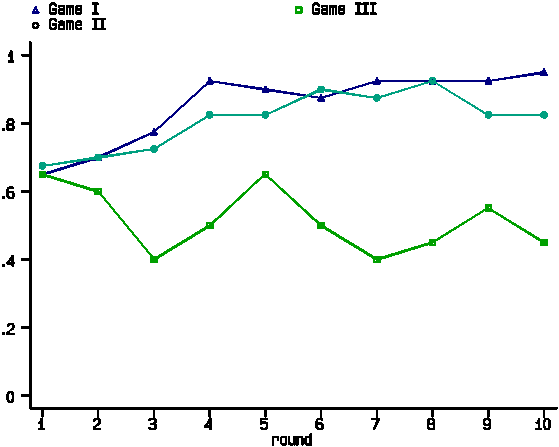
Next we turn to the results from sessions featuring the same Games, but with non-binding pre-play communication. In Figure 4 we present the proportions of Red choices across rounds for these sessions. The results from sessions using the same payoff matrix again appear similar and again we fail to reject the null hypothesis that the proportions of choices of Red are the same across years for both Game I (p=1.000) and Game II (p=0.501). Based on this replicability of choice behavior in our Games with communication, we pool the data from replicate sessions before comparing Games.

----- Figure 4 about here -----

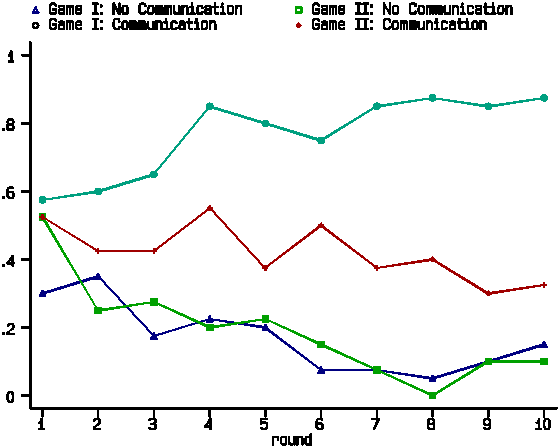
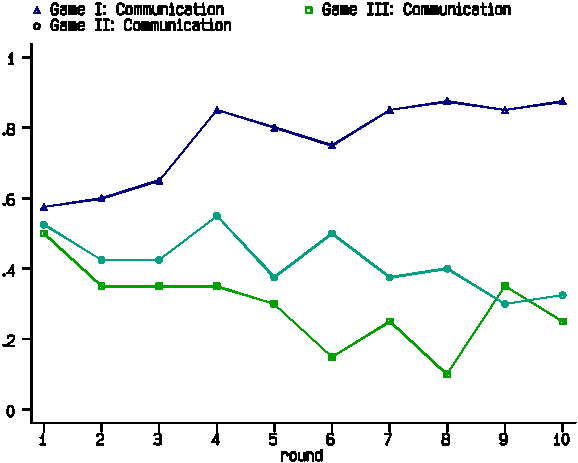
Figure 5 presents the pooled data for Games I and II, with and without communication. It is clear from this Figure that communication increases the propensity to choose Red in both Games, but that the effect is much more marked in Game I. The associated statistical tests confirm this: the proportion of Red choices in Game I is affected by communication (p=0.000), the proportion of Red choices in Game II is also affected by communication (p=0.027), and the proportion of Red choices differs across the two Games with communication (p=0.000). To understand these substantial differences in the choice behavior between Games with communication, we move on to consider subjects' announcements.

----- Figure 5 about here -----

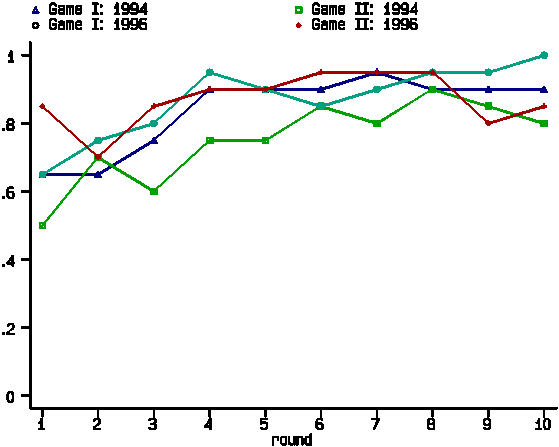
In terms of inducing Red play, it appears that communication is more effective in Game I than Game II. Since communication is introduced by allowing an announcement phase in each Game, the first potential explanation is that announcements differ across Games. In fact, as Figure 6 suggests, in the Games with communication the announcements made by subjects are very similar across all four sessions. Moreover, pairwise comparisons of the proportions of Red announcements across sessions establish replicability for Game I (p=0.487) and for Game II (p=1.000), but also fail to detect differences in announcements across Games (p=0.154). In all four sessions subjects predominantly announce that they will play the Red strategy. Over all four sessions with communication, the proportion of Red announcements climbs from 66% in round 1 to 88% in round 4, and thereafter remains constant.

----- Figure 6 about here -----

Since there is no difference between the outcomes of Games I and II in the absence of communication and since in both Games subjects predominantly announce Red, what then explains the different outcomes in Games I and II with communication? The answer to this question lies in the correlation between announcements and choices. Figure 7 summarizes the interaction between announcement combinations and choices in each Game, pooling across all rounds of both sessions. The data are broken down according to whether the announcement combination preceding each choice was (Red, Red) or not. For example, in Game I 23.25% of choices are Blue, these being comprised of 2.75% following a (Red, Red) announcement combination and 20.5% following some other announcement combination.

----- Figure 7 about here -----

We find that in Game I the following description of how subjects behave fits the data well. First, most subjects announce Red. Second, if the announcement combination is (Red, Red), most subjects choose Red, otherwise they choose Blue. In Game II, as in Game I, most announcements are Red, and subjects tend to choose Blue if anything other than (Red, Red) is announced. However, following a (Red, Red) announcement combination, there is a striking disparity in choice behavior. Unlike in Game I, where the proportion of Red choices conditional on a (Red, Red) announcement combination is more than 96%, in Game II the corresponding conditional proportion is less than 50%.

It is useful to consider the following behavioral rule: if (Red, Red) is announced choose Red, otherwise choose Blue. From Figure 7 we can see that 91.75% of choices in Game I conform to this rule. The consequence of this is that, across all rounds of both sessions of Game I, subjects successfully coordinate on the Pareto-dominant equilibrium 70% of the time with communication (compared with only 2% in the absence of communication). Further, the incidence of disequilibrium outcomes across all rounds and both sessions of Game I with communication is only 13.5% (compared with 30% in the corresponding sessions without communication).

However, in Game II the rule appears to break down: only 57.5% of choices conform. The implication is that while communication increases the amount of coordination on the Pareto-dominant equilibrium, it is much less effective than in Game I. In all rounds of both sessions of Game II, the Pareto-dominant equilibrium outcome is achieved only 18.5% of the time with communication (compared to 5.5% of the time without communication). Also, it is interesting to note that communication does not reduce the incidence of disequilibrium outcomes in Game II: without communication such outcomes occur 27% of the time, with communication they occur 47% of the time.

An explanation for this is that a subject announcing that he or she intends to choose Red is less likely to be believed in Game II. Certainly the data justify such skepticism: after announcing Red subjects choose Red 45% of the time in Game II, compared with 87% of the time in Game I. It may be that subjects fail to follow through on their announcement because the announcement stage results in a disequilibrium announcement combination. It is interesting to note, therefore, that of the subjects who announce Red and choose Blue in Game I, 75% are responding to their opponent announcing Blue. Of subjects who announce Red and choose Blue in Game II, the situation is reversed: only 26% are responding to their opponent announcing Blue.

These results suggest that communication is not sufficient for attaining efficiency in simple coordination games. Although we observe an increase in the amount of efficient play when we introduce communication, the magnitude of the increase is sensitive to the payoffs. In fact, the explanation for this matches Aumann's (1990) conjecture: if a player has a strict preference over his or her opponent's choice, an announcement that he or she intends to make a particular choice can be met with skepticism.

These results prompt the interesting question: Will communication lead to efficient play when players have an incentive to represent themselves truthfully? Perhaps surprisingly, the answer to this question is No. We ran two additional sessions with the parameterization described in Figure 8, one with and one without communication. In this, Game III, payoffs are structured so that a player choosing Blue prefers his or her opponent to also choose Blue, and a player choosing Red prefers his or her opponent to also choose Red.

----- Figure 8 about here -----

In the absence of communication the outcome of this Game is similar to those of the other Games, in that play converges to the risk-dominant equilibrium (see Figure 9). In fact, of the three Games, convergence is strongest in Game III in the sense that while 50% of the subjects chose Red in the first round, after round 6 not a single Red choice was observed.

----- Figure 9 about here -----

It seems reasonable that, since Red announcements are credible in Game III, subjects will announce Red and successfully coordinate on the Pareto-dominant equilibrium in this Game. In fact, and in contrast to the other Games, subjects are almost as likely to announce Blue as Red. The proportion of Red announcements declines from 65% in the first round to 45% in the last round; overall, 48.5% of announcements are Red (see Figure 10).

----- Figure 10 about here -----

Responses to announcements mirror those of Game I - 87.5% of choices are consistent with the rule discussed previously, whereby subjects choose Red if (Red, Red) was announced and choose Blue otherwise. As in Game I communication allows the incidence of coordination failures to be reduced - from 25% to 21%. However, because of the preponderance of Blue announcements, the proportion of Red choices in Game III is lower than in the other Games (see Figure 11), and the subjects coordinate on the (Blue, Blue) equilibrium.

----- Figure 11 about here -----

The high proportion of Blue announcements in Game III can be rationalized by appealing to the observed choice propensities. Figure 12 presents the proportions of Red announcements and the proportions of Red choices conditional on the possible announcement combinations for each Game. Using these sample proportions in place of probabilities, we can estimate the expected payoff from various strategies by first computing the optimal response to a given announcement combination, and then computing the optimal announcement. For example, it can be verified that in Game I, the optimal way to play the Game with communication is to follow the rule discussed earlier, and to announce Red, while in Game II, the optimal way to play is to choose Blue, regardless of announcement combination, and to announce Red.

----- Figure 12 about here -----

In Game III, use of the observed propensities confirms the optimality of choosing Red if (Red, Red) was announced and choosing Blue otherwise: the likelihood of the opponent playing Red is high following (Red, Red), but low following any other announcement combination. Thus, in Game III, optimal play dictates responding to announcements in the same way as in Game I. On the other hand, the optimal announcement for Game III is not so obvious. In fact, the optimal announcement is Blue. This is largely because the payoff from the risk-dominant equilibrium is relatively high. We speculate that reducing this payoff would increase the likelihood of Red announcements and (Red, Red) choices.

5 Conclusion

Our paper addresses the question: When are Nash Equilibria self-enforcing? Aumann has argued that the answer depends on the payoff matrix. Specifically, he suggests that agreements to play a given equilibrium may not be kept if a player has a strict preference over his or her opponent's choice. We investigate the role of communication in coordination games by comparing the efficacy of communication in a game which is not subject to Aumann's critique, Game I, with a game which is subject to it, Game II.

In Game I a subject has no incentive to misrepresent what he or she intends to do. In our sessions with Game I there were 148 occasions when subjects' announcements agreed on Red and the corresponding equilibrium was achieved 137 times (93%). Subjects' announcements agreed on Blue 6 times and all 6 times this equilibrium was achieved. Thus, the empirical evidence for the most part supports the conclusion that Nash Equilibria are self-enforcing in Game I.

In Game II, however, subjects have a strict preference over their opponent's choice. In our sessions with Game II there were 130 occasions when subjects' announcements agreed on Red and the corresponding equilibrium was achieved only 32 times (25%). (For completeness, (Blue, Blue) announcements were followed through on 4 of 6 occasions.) We conclude that Nash Equilibria are not self-enforcing in Game II. Moreover, our results are consistent with Aumann's explanation for this.

We also studied a third Game in which communication may be expected to be most credible in Aumann's sense, because subjects have a positive incentive to represent themselves truthfully. The results from this Game show that for the most part Nash Equilibria are self-enforcing - agreements to play Blue are followed through on 21 of 22 occasions (95%) and agreements to play Red are followed through on 18 of 25 occasions (72%). However, this is not sufficient for communication to select a Pareto-dominant equilibrium. In fact, in this Game many subjects appear to use communication to secure the Pareto-dominated equilibrium. We speculate that in Game III the Pareto-dominated equilibrium payoff is not sufficiently low relative to the efficient equilibrium payoff to tempt subjects to try to secure the higher amount. Clearly testing this conjecture would be a profitable avenue for further research.

Several other directions for the future are also suggested by our results. For example it is interesting to consider how one eliminates 'everyday' interpretations of announcements. Game theory does not embody any concept of trust or honesty. One possibility for further experiments might be to modify the sentences within which the announcements are contained. For example, we speculate that the sentence "I WANT YOU TO CHOOSE Red " would be interpreted differently from the sentence "I INTEND TO CHOOSE Red " in Game II. The first sentence conveys no information regardless of whether trust is important or not, and so should not increase efficient play, while the second sentence may increase efficient play if players attach some importance to keeping one's word.

Other modifications to our basic design could include other communication structures that may enhance the effect of communication, perhaps by mitigating the possibility of confusion arising from disequilibrium announcement combinations. For instance, multi-stage announcements may be more effective than a single stage of announcements, and sequential announcements may be more effective than simultaneous announcements.

As well as these modifications to the experimental design, our results raise deeper questions about the informational environment in which players make strategic choices. Our results suggest that there may be differences between first and last-round behavior in many of the games. Clearly as rounds proceed players will learn not only about the institutional aspects of the game (the payoffs, the order of moves etc.) but will also form beliefs about the population of players from which their opponents are drawn. Modelling this process of learning could yield further insights into the interaction between announcements, choices and beliefs.

Allowing players to communicate prior to playing a game can have important consequences for the outcome of the game. Different communication structures may well have different effects on the observed outcomes and on the process through which these outcomes emerge: this raises interesting possibilities for further research. What our experiments establish is that subjects act strategically when sending and considering messages, and this influences both the messages sent and the actions taken as a result. Therefore, it cannot simply be assumed that free communication will move players towards efficient equilibria.

		Player II
		Blue	Red
Player I	Blue	800,800	800,0
	Red	0,800	1000,1000

Figure 1. Payoff Matrix for Game I.

		Player II
		Blue	Red
Player I	Blue	700,700	900,0
	Red	0,900	1000,1000

Figure 2. Payoff Matrix for Game II.

1

Figure 3. Proportions of Red Choices in Games Without Communication

2

Figure 4. Proportions of Red Choices in Games With Communication

3

Figure 5. Proportions of Red Choices: Pooled Data

4

Figure 6. Proportions of Red Announcements in Games with Communication

Figure 7. Choices and Announcements in Games with Communication (%)

		Player II
		Blue	Red
Player I	Blue	900,900	700,0
	Red	0,700	1000,1000

Figure 8. Payoff Matrix for Game III.

5

Figure 9. Proportions of Red Choices in Games without Communication

6

Figure 10. Proportions of Red Announcements in Games with Communication

7

Figure 11. Proportions of Red Choices in Games with Communication

Figure 12. Observed Decision Propensities

References

Aumann, R.J. (1985): "On the Non-Transferable Utility Value: A Comment on the Roth-Shafer Examples," Econometrica, 53, 667-677.

Aumann, R.J. (1990): "Nash Equilibria Are Not Self-Enforcing," in Economic Decision Making: Games, Econometrics and Optimisation, edited by J.J. Gabszewicz, J.-F. Richard and L.A. Wolsey, Elsevier.

Bernheim, B.D., B. Peleg and M.D. Whinston (1987): "Coalition-Proof Nash Equilibria I: Concepts," Journal of Economic Theory, 42, 1-12.

Cooper, R., D.V. DeJong, R. Forsythe and T.W. Ross (1990): "Selection Criteria in Coordination Games: Some Experimental Results," American Economic Review, 80, 218-233.

Cooper, R., D.V. DeJong, R. Forsythe and T.W. Ross (1992): "Communication in Coordination Games," Quarterly Journal of Economics, 53, 739-771.

Farrell, J. (1988): "Communication, Coordination, and Nash Equilibrium," Economics Letters, 27, 209-214.

Farrell, J. and M. Rabin (1996): "Cheap Talk," Journal of Economic Perspectives, 10, 103-118.

Ferreira, J.L. (1996): "A Communication-Proof Equilibrium Concept," Journal of Economic Theory, 68, 249-257.

Harsanyi, J.C. (1995): "A New Theory of Equilibrium Selection for Games with Complete Information," Games and Economic Behavior, 8, 91-122.

Harsanyi, J.C. and R. Selten (1988): A General Theory of Equilibrium Selection in Games. Cambridge: MIT Press.

Nash, J.F. (1951): "Non-cooperative Games," Annals of Mathematics, 54, 286-295.

Rasmussen, E. (1994): Games and Information. 2nd Edn. Blackwell, Oxford.

Roth, A.E. (1980): "Values for Games Without Side Payments: Some Difficulties with Current Concepts," Econometrica, 48, 457-465.

Straub, P. (1995): "Risk Dominance and Coordination Failures in Static Games," Quarterly Review of Economics and Finance, 35, 339-364..

Van Huyck, J.B., R.C. Battalio and R.O. Beil (1990), "Tacit Coordination Games, Strategic Uncertainty and Coordination Failure," American Economic Review, 80, 234-248.

Appendix A Instructions (Games Without Communication)

General Rules

This is an experiment in the economics of decision making. If you follow the instructions carefully and make good decisions, you can earn a considerable amount of money. You will be paid in private and in cash at the end of the experiment.

At the end of these instructions we will give you a short quiz about the rules of the experiment. The purpose of the quiz is to verify that everybody understands the rules. We cannot begin the experiment until we are certain that everybody understands, so please listen carefully.

There are two rooms of people in this experiment. The people in the other room are hearing exactly the same instructions. The entire experiment will take place through computer terminals, and all interaction between you will take place through the computers. There will be a demonstration round to familiarize you with the computer terminal, DO NOT TOUCH THE KEYBOARD UNTIL THEN. It is important that you do not talk or in any way try to communicate with other people during the experiment. If you disobey the rules, we will have to ask you to leave the experiment.

The experiment will consist of ten rounds. In each round you will be paired with another person who is in the other room. You will never be paired with a person in your own room. You will be paired with a different person in each round. You will not know who is paired with you in any round. Similarly, the other people in this experiment will not know who they are paired with in any round.

You start the experiment with an initial balance of 4200 points. In each round you can earn additional points depending on the decisions made by you and the person you are paired with. At the end of the experiment you will receive £1 for every 1400 points you have earned.

Description of Each Round

At the beginning of each round the computer will tell you the round number, the number of the person that you are paired with, and your point earnings so far. Each round will then consist of three steps: (a) you will make a decision and record it; (b) you will record the decision of the person you are paired with; and (c) you will record your point earnings for the round. We will describe each step in turn.

(a) When everybody is ready to begin the round you will see the statement:

"MY CHOICE IS "

on your terminal. You must select between 1 and 2. You select 1 by pressing the left arrow key, or 2 by pressing the right arrow key. If you want to, you can change your selection using these arrow keys. When you are satisfied with your selection, you will press the Enter key. Once the Enter key has been pressed you will have made your choice and it cannot be changed. You will have 30 seconds to make your choice. After you have made your choice you will record it on your "Record Sheet". You will find this record sheet in your folder. Look at it now. You will record your choices under the column headed "My Choice" on the row for that round.

(b) When both you and the person you are paired with have made your decisions, the computer will inform the other person of your choice, and will inform you of the other person's choice. You will record their choice on your record sheet under the column headed "Other Person's Choice".

(c) The computer will also inform you of your point earnings for the round. You should record these on your record sheet under the column headed "My Point Earnings for this Round". The earnings are calculated according to rules we will discuss below. When you have recorded this information you will press the space bar, to indicate you are ready to begin the next round. When everyone in both rooms has recorded their point earnings the next round will begin.

How your earnings are determined

You will start the experiment with an initial balance of 4200 points. This amount has already been entered in your record sheet. Your additional point earnings in a round will depend on your choice and the choice of the person you are paired with. The point earnings are described in the table below:

	OTHER PERSON CHOOSES 1	OTHER PERSON CHOOSES 2
YOU CHOOSE 1	YOU GET 800 POINTS OTHER PERSON GETS 800 POINTS	YOU GET 800 POINTS OTHER PERSON GETS 0 POINTS
YOU CHOOSE 2	YOU GET 0 POINTS OTHER PERSON GETS 800 POINTS	YOU GET 1000 POINTS OTHER PERSON GETS 1000 POINTS

Thus, if you and the person you are paired with both choose 1 you will each earn 800 points. If you choose 1 and the other person chooses 2 you will earn 800 points and the other person will earn 0 points. If you choose 2 and the other person chooses 1 you will earn 0 points and the other person will earn 800 points. If you and the person you are paired with both choose 2 you will each earn 1000 points.

At the end of round ten, you will add your earnings from each round to your initial balance and enter the total on the bottom line of your record sheet. This will determine your total point earnings. At the end of the experiment you will receive £1 for every 1400 points you earned.

Demonstration Round

We will demonstrate how you make your choices on the computer. Please press the space bar now and look at the screen. The screen tells you which is the current round, and your subject number. If this was not simply a demonstration round, the next line would tell you the subject number of the person you are paired with for this round. The next line is for your choice. The cursor is flashing, indicating that you must make a choice. Press the left arrow. You will see that 1 has been selected. Now press the right arrow. This will change your selection to 2. You can change your selection as many times as you want using the arrow keys. Press the Enter key. Now you have made your choice, and you should record it on your record sheet on the row labelled "Demonstration". When everyone has made their choice, the next screen will appear.

If this was not simply a demonstration round, the computer would inform you of the choice made by the person you were paired with and your point earnings. You would then record these on your record sheet. Before we begin round one, I will give you an opportunity to ask questions, and then I will ask you to complete the quiz that you will find in your folder.

Are there any questions?

Appendix B Instructions (Games With Communication)

General Rules

This is an experiment in the economics of decision making. If you follow the instructions carefully and make good decisions, you can earn a considerable amount of money. You will be paid in private and in cash at the end of the experiment.

At the end of these instructions we will give you a short quiz about the rules of the experiment. The purpose of the quiz is to verify that everybody understands the rules. We cannot begin the experiment until we are certain that everybody understands, so please listen carefully.

There are two rooms of people in this experiment. The people in the other room are hearing exactly the same instructions. The entire experiment will take place through computer terminals, and all interaction between you will take place through the computers. There will be a demonstration round to familiarize you with the computer terminal, DO NOT TOUCH THE KEYBOARD UNTIL THEN. It is important that you do not talk or in any way try to communicate with other people during the experiment. If you disobey the rules, we will have to ask you to leave the experiment.

The experiment will consist of ten rounds. In each round you will be paired with another person who is in the other room. You will never be paired with a person in your own room. You will be paired with a different person in each round. You will not know who is paired with you in any round. Similarly, the other people in this experiment will not know who they are paired with in any round.

You start the experiment with an initial balance of 4200 points. In each round you can earn additional points depending on the decisions made by you and the person you are paired with. At the end of the experiment you will receive £1 for every 1400 points you have earned.

Description of Each Round

At the beginning of each round the computer will tell you the round number, the number of the person that you are paired with, and your point earnings so far. Each round will then consist of five steps: (a) you will make an announcement and record it; (b) you will record the announcement of the person you are paired with; (c) you will make a decision and record it; (d) you will record the decision of the person you are paired with; and (e) you will record your point earnings for the round. We will describe each step in turn.

(a) When everybody is ready to begin the round, you will see the statement:

"I INTEND TO CHOOSE "

on your terminal. You must select between 1 and 2. You select 1 by pressing the left arrow key, or 2 by pressing the right arrow key. If you want to, you can change your selection using these arrow keys. When you are satisfied with your selection, you will press the Enter key. Once the Enter key has been pressed you will have made your announcement and it cannot be changed. You will have 30 seconds to make your announcement. After you have made your announcement you will record it on your "Record Sheet". You will find this record sheet in your folder. Look at it now. You will record your announcement under the column headed "My Announcement" on the row for that round.

(b) When everybody has made their announcement, the computer will inform you of the announcement of the person you are paired with. On your terminal, you will see either the statement:

"THE SUBJECT YOU ARE PAIRED WITH INTENDS TO CHOOSE 1 "

if the subject with whom you are paired announced 1, or:

"THE SUBJECT YOU ARE PAIRED WITH INTENDS TO CHOOSE 2 "

if the subject with whom you are paired announced 2. You will then record the announcement on your "Record Sheet". You will record the announcement under the column headed "Other Person's Announcement" on the row for that round. When you have recorded this information you will press the space bar, to indicate you are ready to begin the next part of the round.

(c) When everybody is ready to continue the round, you will see the statement:

"MY CHOICE IS "

on your terminal. You must select between 1 and 2. You select 1 by pressing the left arrow key, or 2 by pressing the right arrow key. If you want to, you can change your selection using these arrow keys. When you are satisfied with your selection, you will press the Enter key. Once the Enter key has been pressed you will have made your choice and it cannot be changed. You will have 30 seconds to make your choice. After you have made your choice you will record it on your "Record Sheet". You will record your choice under the column headed "My Choice" on the row for that round. You are not required to make the choice announced earlier.

(d) When both you and the person you are paired with have made your decisions, the computer will inform the other person of your choice, and will inform you of the other person's choice. You will record their choice on your record sheet under the column headed "Other Person's Choice".

(e) The computer will also inform you of your point earnings for the round. You should record these on your record sheet under the column headed "My Point Earnings for this Round". The earnings are calculated according to rules we will discuss below. When you have recorded this information you will press the space bar, to indicate you are ready to begin the next round. When everyone in both rooms has recorded their point earnings the next round will begin.

How your earnings are determined

You will start the experiment with an initial balance of 4200 points. This amount has already been entered in your record sheet. Your additional point earnings in a round will depend on your choice and the choice of the person you are paired with. The point earnings are described in the table below:

	OTHER PERSON CHOOSES 1	OTHER PERSON CHOOSES 2
YOU CHOOSE 1	YOU GET 1000 POINTS OTHER PERSON GETS 1000 POINTS	YOU GET 0 POINTS OTHER PERSON GETS 800 POINTS
YOU CHOOSE 2	YOU GET 800 POINTS OTHER PERSON GETS 0 POINTS	YOU GET 800 POINTS OTHER PERSON GETS 800 POINTS

Thus, if you and the person you are paired with both choose 1 you will each earn 1000 points. If you choose 1 and the other person chooses 2 you will earn 0 points and the other person will earn 800 points. If you choose 2 and the other person chooses 1 you will earn 800 points and the other person will earn 0 points. If you and the person you are paired with both choose 2 you will each earn 800 points.

At the end of round ten, you will add your earnings from each round to your initial balance and enter the total on the bottom line of your record sheet. This will determine your total point earnings. At the end of the experiment you will receive £1 for every 1400 points you earned.

Demonstration Round

We will demonstrate how you make your announcements and choices on the computer. Please press the space bar now and look at the screen. The screen tells you which is the current round, and your subject number. If this was not simply a demonstration round, the next line would tell you the subject number of the person you are paired with for this round. The next line is for your announcement. The cursor is flashing, indicating that you must make an announcement. Press the left arrow. You will see that 1 has been selected. Now press the right arrow. This will change your selection to 2. You can change your selection as many times as you want using the arrow keys. Press the Enter key. Now you have made your announcement, and you should record it on your record sheet on the row labelled "Demonstration". When everyone has made their announcement, the next screen will appear.

If this was not simply a demonstration round, the computer would inform you of the announcement made by the person you were paired with. You would then record this on your record sheet. Now press the space bar and look at the next screen.

The screen tells you which is the current round and your subject number. If this was not simply a demonstration round, the next line would tell you the subject number of the person you are paired with for this round. The next line is for your choice. The cursor is flashing, indicating that you must make a choice. Press the left arrow. You will see that 1 has been selected. Now press the right arrow. This will change your selection to 2. You can change your selection as many times as you want using the arrow keys. Press the Enter key. Now you have made your choice, and you should record it on your record sheet on the row labelled "Demonstration". When everyone has made their choice, the next screen will appear.

If this was not simply a demonstration round, the computer would inform you of the choice made by the subject you were paired with and your point earnings. You would then record these on your record sheet. Before we begin round one, I will give you an opportunity to ask questions, and then I will ask you to complete the quiz that you will find in your folder.

Are there any questions?