Testing between Different Types of
Switching Regression Models

During the last years a number of methodological papers on models with periodic discrete parameter shifts have revived interest in these so-called regime switching models and have inspired much applied work in various branches of economics. Different types of switching models are in use, and in many cases the use of a particular model type is not justified on statistical grounds. This paper suggests a new procedure to test between different types of such models based on embedding these models within a more general one. First simulation results of the quality of this test are presented, and finally directions for further research are suggested.

Contents

1 Regime Switching Models 22 Threshold Models as Restrictions of (z) and (z) Models 43 Tests between nonnested regime switching models 7 References 9

1. Regime Switching Models

Since the beginning of the 70's econometricians have been interested in various types of generalised regression models which admit different, discretely changing parameter values at different time periods, so-called regime switching models. The basic types which are in use where introduced by Goldfeld and Quandt (1973). They can roughly be categorised as follows:

• Models where the change in regime is determined by an observed variable.

Among these the most important ones are threshold models, where the state changes when an observed variable z passes a threshold c. The first economic application of this model type is probably Fair and Jaffee (1972). Threshold models have received renewed attention since the work of Tong and others about time series models which incorporate the threshold principle, the so called (self-exciting) threshold autoregressive ((SE)TAR) models, cf. Tong (1983) and (1990). Potter (1995) gives an application on the US GNP time series (but Hansen (1996) doubts that the data actually exhibit two distinct states).

• Models where the change in regime cannot be observed directly.

When the generating principle of the switching process is not known, it must be modelled separately (i.e. usually: independently) from the observed variables. Two specifications are prominent in the literature:

• Models where the current state is independent of the other states and the probability of a certain state does not change over time („Bernoulli", „simple switching" or „i.i.d. switching" models; Goldfeld and Quandt call this modelling strategy the „-method", being the probability of one of the states).
• Models where the current state depends only on the previous state, i.e. the states follow a Markov chain („-method"). Well-known econometric applications are Goldfeld and Quandt (1973) or Cosslett and Lee (1985). Again, turning the focus on time series models with an underlying Markov chain which determines the sequence of states has inspired many economic applications since the late 80's. For methodological considerations cf. Hamilton (1989 ff.). Among the abundance of economic applications Engel and Hamilton (1990) and Cecchetti, Lam and Mark (1990) are frequently cited.

• Hybrid models combining these mechanisms.

Goldfeld and Quandt (1973) already suggested Bernoulli and Markov models with the probability of a certain state () respectively the transition probability () depending on an observed variable z („(z)", „(z)"). These where re-introduced by Lee (1991), Diebold, Lee and Weinbach (1994), Filardo (1994) and others. Usually the dependency of the state probability on the observed variable z is parameterised by a logistic function or the cumulative density function (c.d.f.) of a probability distribution.

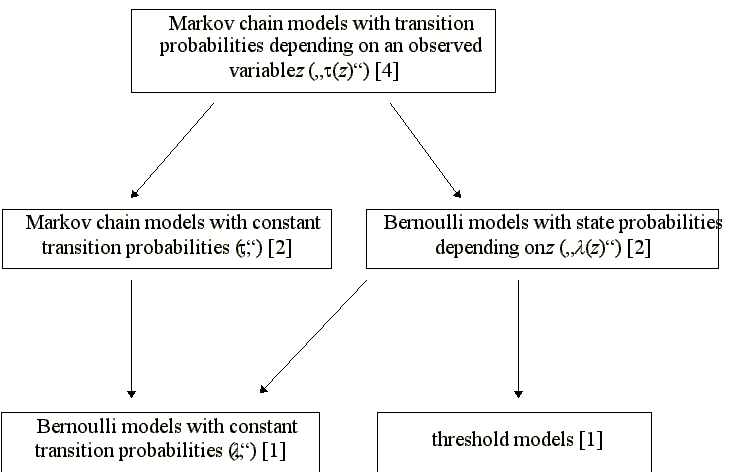
Figure 1 gives a systematic overview of these model types (parameter restrictions are marked by an arrow).

Before modelling data with a regime switching model, one should generally check whether the existence of several states is really statistically significant, i.e. test the nested null hypotheses of no change in state. In constructing such tests, one is always confronted with the difficult problem that some of the parameters of the model are not identified under the null hypotheses. A lot of research has been dedicated to this problem, mostly adopting the approach of Davies (1977, 1987). For tests against threshold models cf. e.g. Tsay (1989), Chan (1990), Tong (1990), p. 233-251, and Hansen (1996). Hansen (1992) proposes a test against Markov models which seems to be difficult to implement, cf. his Erratum (1995). Garcia (1995) applies the procedure developed by Hansen (1995) for threshold models to Markov models.

Instead of adding to the existing literature on this issue, this paper addresses the problem of testing between different types of switching regression models. This is motivated primarily by two observations:

• The problem of testing the null of a model without regime shift is far from being settled and the tests proposed until now seem either not very powerful or difficult to implement, so that many (in fact most) authors of applied papers decide to use a model with several states on purely theoretical grounds. In most cases, the theory does not point to a specific model and so one of the various model types is selected ad hoc (a classical example are the competing models for the US housing market by Fair and Jaffee (1972), Quandt (1972) and Goldfeld and Quandt (1973).
• When the null of a model without regime shift is tested, it does happen that different types of models are significant, e.g. a Bernoulli model in Hansen (1992) and a threshold model in Potter (1995), both for US GNP.

The existing literature on switching regression models does not pay attention to the fact that the two hybrid model types („(z)" and „(z)") restrict to threshold models. In what follows the author proposes to investigate and exploit this observation in the context of testing between different types of regime switching models.

1. Threshold Models as Restrictions of (z) and (z) Models

The restriction (z) (z) is analogous to the restriction which is well-known in the literature (cf. e.g. Cosslett and Lee (1985), p. 83 ff.). When testing this restriction, one poses the question whether the data show a significant persistence of the states rather than an independent pattern. The standard asymptotic tests (LQ, LM and Wald) are applicable here in the sense that the corresponding test statistics are asymptotically distributed as ². Hamilton (1996), p. 139 f., proposes a Newey-Tauchen-White test for this restriction.

The asymptotic theory applies equally well to the restrictions (z) and (z) . Here the influence of z on the state respectively the transition probabilities is tested.

The situation is more intricate with the restriction (z) [threshold models] and
(z) [threshold models]. The latter case will be treated first. Here one asks whether the threshold principle suffices to explain the changes in state or whether another, latent mechanism seems to be significant in the data.

A generally accepted candidate for (z) is the c.d.f. of the normal distribution:

.

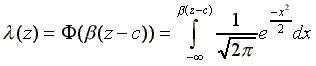In the limit case this becomes a (Heaviside) step function with a discontinuity at
z = c and the corresponding model is a threshold model. The regularity conditions for the theorem about the asymptotic distribution of the usual test statistics (cf. e.g. Kendall and Stuart (1973), p. 241) are not fulfilled in this case and the theorem is not directly applicable. Nevertheless one would intuitively suspect that it applies here as well, but the author does not know a proof.

Whether or not a proof of this generalisation of the classical theorem is available, it would be interesting to have an idea about the finite-sample distribution of the test statistics to compare the nominal and the actual size of the test.

In the following, the first results of a limited Monte Carlo study are presented which give a first idea of the outcomes of a large-scale simulation study which needs to be conducted.

To simulate the distribution of the test statistics under the null hypotheses, 250 samples containing each 100 observations of a threshold model were generated and the LQ and the Wald statistic were calculated. The true model was one without autoregressive dynamics, without heteroscedasty or exogenous regressors:

and the alternative the corresponding (z) model:

,

with

.

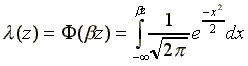The variable z was simulated by independent realisations of a standard-normally distributed variable.

The values of the Wald statistic were extremely small for some of the parameter values. A possible explanation for this phenomenon is a lack of accuracy in the numerical computation of the matrix of derivatives of the log-likelihood function and its inversion. In subsequent studies, it might be favourable to work with the analytical derivatives of Gable, van Norden and Vigfusson (1995) and Hamilton (1996).

The results for the LQ statistic can be summarised as follows:

• When using a sample length of T = 100 its values tend to be slightly smaller than the expected ²(1). As yet it is an open question weather this indicates that the above conjecture does not hold or whether this is rather due to the small sample length or to the imperfectness in the search algorithm for the global maximum of the log-likelihood function under the alternative (a non-linear gradient method combined with a grid search for = 1/ ). Possibly different algorithms, e.g. the EM algorithm of Dempster, Laird and Rubin (1977), Ruud (1991) and Hamilton (1990) yield better results.
• The quality of the approximation seems to depend only on the ratio of the standard deviation of the noise process to the difference between the means of the two states.

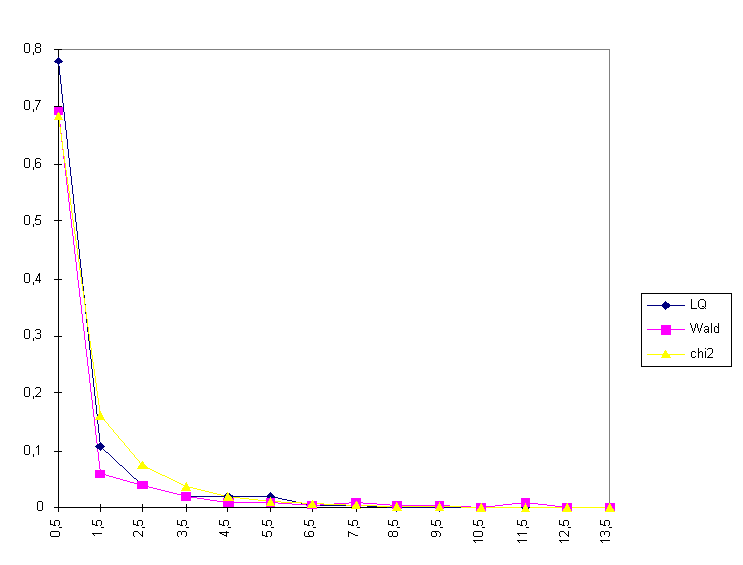
For a graphical display of the empirical distribution of the test statistics see Figure 2.

As for the power of this test, another simulation was conducted with the alternative as the true model. Figure 3 gives the relative rejection frequencies at different parameter values. According to the first study, the critical value of the test at a 5%-level is approximately 3.0 which was adopted for this simulation.

These first results can be summarised as follows: The simulations support the conjecture of an asymptotic ²(1)-distribution of the LQ statistic, and the test seems to have acceptable power for moderate values of and not too small differences in the two means (relative to the standard deviation).

As far as the restriction (z) [threshold models] is concerned, it should be noted that the corresponding LQ statistic is the sum of that of the tests of the restrictions (z) (z) and
(z) [threshold models]. The test statistic for the first of these two restrictions is definitively asymptotically distributed as ²(2) (in the usual parameterisation), so if the above conjecture for the second restriction holds, the sum will be asymptotically distributed as ²(3). The situation should be similar with the LM and the Wald statistic since these are approximations of the LQ statistic.

There remain many open questions for future research:

• What happens when one uses more complicated data generating processes?
  • For practical considerations, linear models with exogenous regressors and time series models are most important.
  • It would be interesting to include heteroscedastic models as it may well be the case that a shift in variance is an important feature of the different states of the economy. Here the work of Kiefer (1987, 1980) is relevant.
  • Phillips (1995) uses bivariate Markov models, Granger and Teräsvirta (1993) bivariate STAR models to describe two economies jointly.
  • The number of possible states need not be restricted to two. Garcia and Perron (1996) argue that a model with three states be appropriate for US interest rates.
• Does the quality of the approximation improve when the maximum of the log-likelihood function is calculated with the EM algorithm?
• In this situation the Lagrange multiplier statistic cannot be defined in the ordinary way due to the above-mentioned discontinuity at = . Does its limit value for
  exist and what can be said about its (asymptotic) distribution? Some results in this direction would be very helpful from the practical point of view since the LM statistic can be calculated without fitting the alternative model. Alternatively, is it possible to construct „LM-type tests" in the spirit of Luukkonen, Saikkonen and Teräsvirta (1988)?
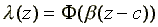• Can the test be generalised to the case where the threshold parameter c has to be estimated? A model which specialises to such a threshold model and a model is one with and a variable and c.
• A number of variants of the basic models have been suggested to which the test could possibly be applied:
  • Lee (1991) also considers different functional forms of (z) which could prove especially interesting when z = t and the corresponding threshold model is a model of structural break. This should be seen in analogy to the test for structural break which Lin and Teräsvirta developed using STAR models, cf. Teräsvirta and Lin (1995).
  • Durland and McCurdy (1994) propose a very interesting model where z represents the time the system has remained in the actual state. This is designed for situations in which a change in state becomes more and more likely the more time has passed since the last switch.

1. Tests between nonnested regime switching models

The last paragraph exclusively dealt with the problem of testing between nested switching regression models. The case of nonnested models is probably the more interesting one. The most prominent model types in the existing applied literature are Markov and threshold models, and the use of a certain model type is rarely justified statistically. This applies especially to time series models.

A lot of research has been dedicated to the problem of testing between nonnested models (for an overview cf. e.g. McAleer (1995)). To the author's knowledge as yet only one paper dealt with the special problem of testing between nonnested switching regression models, namely the (unpublished) paper of M. Pesaran and Potter (1991) who used a rather sophisticated simulation technique, developed by M. Pesaran and B. Pesaran (1993), to test between Markov and threshold models.

The first strategy one would adopt in such a situation is probably that described in many econometrics textbooks (cf. e.g. Harvey (1993), p.177 ff.), namely to look for a more general model within which both competing models are embedded. One can then test the two restrictions separately with conventional tests (if available). If one restriction is rejected and the other one is not, one should clearly favour the second restricted model. If none of the two tests reject the respective null hypotheses this means that the sample is too small to allow a definite conclusion to be drawn. What distinguishes this testing procedure from other methods is the fact that if both separate tests reject the null a consistent and interpretable alternative is at hand, namely the embedding model.

Figure 1 reveals that this procedure indeed offers a way to test between competing nonnested regime switching models. In particular, one could test between Markov and threshold models if the restriction (z) [threshold models] was testable with conventional tests as conjectured in chapter 2.

However, before this test can be used in practice, one should check out via simulations

• which levels for the separate conventional tests one should choose and how this influences the various error probabilities
• how good the test is in detecting the correct model.

Another interesting field of application is that of business cycle analysis using SETAR- and Markov-switching time series models. It would be interesting to use the test to compare e.g. Hamilton's (1989) and Potter's (1995) models of US GNP. Another step in this direction is the work by Clements and Krolzig (1996).

References

CECCHETTI, S. G., LAM, P.-S. and MARK, N. C. (1990): Mean Reversion in Equilibrium Asset Prices, American Economic Review 80 (1990), p. 398-418

CHAN, K. S (1990): Testing for Threshold Autoregression, The Annals of Statistics 18 (1990), p. 1886-1894

CLEMENTS, MICHAEL P. und KROLZIG, HANS-MARTIN (1996): A Comparison of the Forecast Performance of Markov-switching and Threshold Autoregressive Models of US GNP, Working Paper presented at a poster session of the 8th EC2-Conference in Firenze (13./14.12.1996)

COSSLETT, STEPHEN R. and LEE, LUNG-FEI (1985): Serial Correlation in Discrete Variable Models, Journal of Econometrics 27 (1985), p. 79-97

DAVIES, R. B. (1977): Hypothesis Testing When a Nuisance Parameter is Present Only Under the Alternative, Biometrika 64 (1977), p. 247-254

(1987): Hypothesis Testing When a Nuisance Parameter is Present Only Under the Alternative, Biometrika 74 (1977), p. 33-34

DEMPSTER, A. P., LAIRD, N. M. and RUBIN, D. B. (1977): Maximum Likelihood from Incomplete Data via the EM Algorithm, Journal of the Royal Statistical Society (Series B) 39 (1977), p. 1-38)

DIEBOLD, FRANCIS X., LEE, JOON-HAENG and WEINBACH, GRETCHEN C. (1994): Regime Switching with Time-Varying Transition Probabilities, in: HARGREAVES, COLIN (Hrg.): Non-Stationary Time Series Analysis and Cointegration, Oxford 1994, p. 284-302 (Oxford University Press)

DIEBOLD, FRANCIS X. and RUDEBUSCH, GLENN D. (1996): Measuring Business Cycles: A Modern Perspective, The Review of Economics and Statistics 78 (1996), p. 67-77

DURLAND, J. MICHAEL and MCCURDY, THOMAS H. (1994): Duration Dependent Transitions in a Markov Model of U.S. GNP Growth, Journal of Business and Economic Statistics 12/3 (1994), S 279-288

ENGLE, CHARLES and HAMILTON, JAMES D. (1990): Long Swings in the Dollar: Are They in the Data and Do Markets Know It?, American Economic Review 80 (1980), p. 689-713

FAIR, R. C. and JAFFEE, D. M. (1972): Methods of Estimation for Markets in Disequilibrium, Econometrica 40 (1972), P. 497-514

FILARDO, ANDREWS J. (1994): Business Cycle Phases and their Transitional Dynamics, Journal of Business and Economics Statistics 3 (1994), p. 299-308

GABLE, JEFF, VAN NORDEN, SIMON and VIGFUSSON, ROBERT (1995): Analytical Derivatives for Markov Switching Models, Bank of Canada Working Papers 95-7 (1995)
(ewp-ge/9508001)

GARCIA, RENÉ (1995): Asymptotic Null Distribution of the Likelihood Ratio Test in Markov Switching Models, Cahiers de recherche 1095 (1995), Centre de recherche et développement en économique, Université de Montréal

and PERRON, PIERRE (1996): An Analysis of the Real Interest Rate under Regime Shifts, The Review of Economics and Statistics 78 (1996), p. 111-125

GOLDFELD, STEPHEN M. and QUANDT, RICHARD E. (1973): A Markov Model for Switching Regressions, Journal of Econometrics 1 (1973), p. 3-16

GRANGER, G. W. J. and TERÄSVIRTA, T. (1993): Modelling Nonlinear Economic Relationships, Oxford 1993 (Oxford University Press, Advanced Texts in Econometrics)

HAMILTON, JAMES D. (1989): A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle, Econometrica 57 (1989), p. 357-84

(1990): Analysis of Time Series Subject to Changes in Regime, Journal of Econometrics 45, p. 39-70

(1993): Estimation, Inference, and Forecasting of Time Series Subject to Changes in Regime, in: MADDALA, C. S., RAO, C. R., and VINOD, H. D. (Hrg.): Econometrics (Handbook of Statistics Vol. 11), Amsterdam 1993, p. 231-260 (North-Holland)

(1994): Time Series Analysis, Princeton 1994 (Princeton University Press)

(1996): Specification Testing in Markov-Switching Time-Series Models, Journal of Econometrics 70 (1996), p. 127-157

HANSEN, BRUCE E. (1992): The Likelihood Ratio Test under Non-Standard Conditions: Testing the Markov-Switching Model of GNP, Journal of Applied Econometrics 7 (Supplement) (1992), p. 61-82

(1995): Erratum, Boston College Working Papers in Economics

(1996): Inference When a Nuisance Parameter Is Not Identified under the Null Hypothesis, Econometrica 64 (1996), p. 413-430

HARVEY, ANDREW C. (1993): Time Series Models, New York 1993 (Harvester Wheatsheaf)

HENDRY, DAVID (1984): Monte Carlo Experimentation in Econmetrics, in: GRILICHES, ZWI and INTRILIGATOR, MICHAEL D. (1984): Handbook of Econometrics (Handbook in Economics Book 2) Vol.2, p. 937-976, Amsterdam 1984 (North-Holland)

KENDALL, MAURICE G., and STUART, ALAN (1973): The Advanced Theory of Statistics, Vol.2: Inference and Relationship, London 1973

KIEFER, NOCHOLAS M. (1978): Discrete Parameter Variation: Efficient Estimation of a Switching Regression Model, Econometrica 46 (1978), p. 427-434

(1980): A Note on Switching Regression and Logistic Discrimination, Econometrica 48 (1980), p. 1065-1069

LEE, JOON-HANEG (1991): Nonstationary Markov Switching Models of Exchange Rates: The Pound-Dollar Exchange Rate, Dissertation, University of Pensilvania 1991

LIN, CHIEN-FU and TERÄSVIRTA, T. (1994): Testing the Constancy of Regression Parameters Against Continuous Structural Change, Journal of Econometrics 62 (1994), p. 211-228

LUUKKONEN, R., SAIKKONEN, P. and TERÄSVIRTA, TIMO (1988): Testing Linearity Against Smooth Transition Autoregressive Models, Biometrika 75, p. 491-499

MCALEER, MICHAEL (1995): The Significance of Testing Empirical Nonnested Models, Journal of Econometrics 67 (1995), p. 149-171

NORDEN, SIMON VAN and SCHALLER, HUNTLEY (1993): Regime Switching in Stock Market Returns, Bank of Canada Working Papers (ewp-em/9502002)

PESARAN, B. and PESARAN, M. HASHEM (1993): A Simulation Approach to the Problem of Computing Cox's Statistic for Non-nested Models, Journal of Econometrics 57 (1993), p. 377-392

PHILLIPS, KERK L. (1991): A Two-Country Model of Stochastic Output with Changes in Regime, Journal of International Economics 31 (1991), p. 121-142

POTTER, SIMON M. (1995): A Nonlinear Approach to US GNP, Journal of Applied Econometrics 10 (1995), p. 109-125

QUANDT, R. E. (1972): A New Approach to Estimating Switching Regressions, Journal of the American Statistical Association 67 (1972), p. 306-310

(1982): Econometric Disequilibrium Models, Econometric Reviews 1(1) (1982), S. 1-63

RUUD, PAUL A. (1991): Extension of Estimation Methods Using the EM-Algorithm, Journal of Econometrics 49 (1991), p. 305-341

SAIKKONEN, P. and LUUKKONEN, R. (1988): Lagrange Multiplier Tests for Testing Non-Linearities in Time Series Models, Scandinavian Journal of Statistics 15, p. 55-68

TERÄSVIRTA, TIMO (1994): Specification, Estimation, and Evaluation of Smooth Transition Autoregressive Models, Journal of the American Statistical Association 89, p. 208-218

and LIN, CHIEN-FU (1995): TESTING Parameter Constancy in Linear Models Against Stochastic Stationary Parameters, Humbold-Universität Berlin, SFB 373, Discussion Papers 57

TONG, HOWELL (1983): Threshold Models in Non-Linear Time Series Analysis, New York 1983 (Springer Lecture Notes in Statistics 21)

(1990): Nonlinear Time Series: A Dynamical System Approach, Oxford 1990 (Oxford University Press)

TSAY, RUEY S. (1989): Testing and Modelling Threshold Autoregressive Modells, Journal of the American Statistical Association 84 (1989), p. 231-240