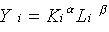 i {1,2,...,m} , > 0, + < 1 (1)
i {1,2,...,m} , > 0, + < 1 (1)
In addition to supervision
costs, the labor cost of an enterprise (plantation) in the system
of slavery consists of the cost of acquiring the slaves and the
subsistence compensation given out to the slaves. In this paper,
we leave aside the issue of supervision costs previously taken
up in the theoretical literature on slavery, and focus on these
two peculiar components of labor costs. We analyze the implications
of this cost structure on the levels of profitability, efficiency
and determination of equilibrium wages, and compare them to systems
with free labor markets, along a continuum of demand side Cournotic
competition. For this purpose, we first use a model characterized
by a decreasing returns to scale technology, and show, parallel
to the findings of Vedder, et. al. (1990), that the equilibrium
subsistence wage in the system of slavery is strictly lower than
the marginal product of labor. We then extend the model, given
the same technology and preferences, to free labor markets covering
possibilities ranging from monopsony to perfect competition in
the limit, and obtain a second and perhaps more striking result:
Differently from equilibria in imperfectly competitive free labor
markets, slavery and perfect competition equilibria are Pareto
optimal. Furthermore, our comparisons across labor market scenarios
suggest that the resistance of slaveholders to the abolishment
of slavery is directly related to the expected level of demand
side competition in the free labor market which would replace
slavery. Finally, we show that the conclusions derived from our
analysis would remain generally valid under a constant returns
to scale technology as well.
Keywords: Economics of Slavery vs. Free Labor Systems, Labor Economics, Perfect Competition vs. Oligopsony and Monopsony in Labor Markets.
----------------
*
Comments on an earlier
draft by Prof. Gavin Wright are greatly appreciated but the responsibility
for any errors or omissions that might have remained belongs to
the authors.Introduction
The political economy of slavery has been a widely discussed topic in economic history literature, particularly in reference to the North American experience. Findlay (1975) characterizes slavery as one of the oldest, most complex and extensive of the institutions in economic history. Wright (1991 and 1997) identifies three distinct dimensions of the subject, each providing material for extensive historical investigation: slavery as a work organization or a system of production; slavery as a set of property rights, and slavery as a political regime. Depending upon the purpose at hand, a recognition of these distinct dimensions could help with the choice of proper level of abstraction, leading to a better understanding of the economics or politics of slavery through a confinement of analytical focus. Taken as a system of production, for example, slavery may be viewed strictly as a special type of factor market organization, and economic implications of using slave labor may be evaluated in comparison to alternative forms of labor market structures. While the wide range of labor employment practices observed under the name of slavery may limit the historical relevance of results from such an evaluation to a certain locale, period or produce, there obviously are certain features and common practices essentially distinguishing slavery from others. The purpose of this paper is to present a formal comparison of slavery to free labor economies by focusing on some of the factor market characteristics that are essentially different across systems, and to discuss certain microeconomic implications of these characteristics. Such a comparison might help historical analysis aiming to explain the economic reasons behind the rise and collapse of slavery as a work organization.
While the multifarious structure of slavery as an economic institution has always attracted the attention of economists, the aspect most extensively investigated has been the profitability/efficiency issue, particularly within the US context. The empirical evidence reported in the literature, however, has failed to lead to a consensus among researchers about the conclusions that could be derived. Instead, the controversy around the issue grew especially after the publication in 1974 of Time on the Cross by Fogel and Engerman, where the authors argued in reference to North American agriculture that the production in the South was more efficient than in the North. According to Fogel and Engerman (1974), this regional difference was due to the higher physical efficiency of slave farms located mostly in the South, relative to free farms in the North. The efficiency advantages of slave farms, in turn, could be attributed to the larger scale of plantation operations and superior managerial skills of planters. In a follow up article, Fogel and Engerman (1977) argued more specifically that efficiency differences followed from higher intensity per unit of time of slave labor relative to free workers, rather than longer hours worked by slaves or lower costs associated with slave labor. Reactions to Fogel and Engerman's work came from Wright (1976 and 1979), Haskell (1979), David and Temin (1979), Schaefer and Schmitz (1979), and Field (1988) each focusing on a different aspect of the original work. Wright (1976 and 1979) and David and Temin (1979), for example, challenged the validity of efficiency calculations presented in the 1977 article with reference to the choice of data and the crop mix considered, whereas Field (1988) proposed an alternative specification for the production function to avoid problems in the Fogel and Engerman formulation. Schaefer and Schmitz (1979), on the other hand, agreed that the suggested relationship between the use of slave labor and productivity could indeed be explained by the scale of operation, but challenged the line of reasoning behind the conclusions drawn. According to them, slaves were not the cause of higher productivity, but rather a means of achieving a larger scale of operation which, in turn, led to higher levels of profitability.
Despite such a sizable empirical literature that continues to grow, relatively few studies have been devoted to a theoretical analysis of the issue, e.g., Fleisig (1976), with most of the theoretical works focusing on pain-incentive aspects and supervision costs, e.g., Findlay (1975), Fenoaltea (1984), Chwe (1990). Others have presented formal models developed for broader comparisons of slavery to free labor economies in terms of Pareto-superiority and welfare implications, e.g., Dirickx and Sertel (1978), de Dios (1990). This paper aims to contribute to this literature by presenting a theoretical, factor market analysis of slavery in comparison to other economic systems where labor is self-owned -as opposed to being owned by others in the words of Graves, et. al. (1983). A salient feature of the comparative analysis here is that it does not consider the somewhat ambiguous notion of free labor as a single benchmark. Free labor economies are characterized, instead, by labor markets that are perfectly competitive on the supply side, but competitive to differing degrees on the demand side. While ignoring supervision or monitoring costs studied in the previous literature, our analysis of labor costs emphasizes the quasi-capital structure of the slaves by relating slave prices to returns on capital. The analytical results concerning the levels of profitability, efficiency and labor compensation under slavery are also contrasted with the results of previous studies evaluating the issues from a historical/empirical perspective. However, given the extensive scope of the term slavery, the empirical relevance of analytical results would be limited to the cases where the definition of slavery employed is applicable. To avoid confusion, the term slavery is used in the rest of the discussion strictly to refer to a system of production where human labor needed for production is supplied by slaves who could be purchased and sold in the market just like any other factor of production, and once purchased (or inherited), are required to perform the tasks assigned to them by their owners, without having the will to quit working.
The analytical framework
employed here is an extended version of the "nutshell"
analysis which was developed by Dirickx and Sertel (1978) for
a comparative evaluation of certain key variables in different
political economies characterized by different objective functions
and constraints. In comparing the political economies they consider,
Dirickx and Sertel (1978) assume that the societies living under
each political economy are equipped with the same technology,
resources and preferences. The same assumption is employed here
so as to assure comparability across systems. Greater detail about
the assumptions on common and differing features of each system
is given in the next section. Sections 3 and 4 develop the model
for the system of slavery and free labor economies, respectively.
Section 5 discusses results and presents concluding remarks.
Preliminaries
The steps of model development here are similar to Dirickx and Sertel (1979) but significant variations are introduced to the model structure. Some assumptions are commonly employed throughout the analysis regardless of whether the labor force of the system under consideration is made up of slaves or free workers. The agents are assumed to be symmetric. The number of firms and the number of workers/slaves in each system are m and N (=mn), respectively, where n is the number of workers (slaves) employed by each enterprise under the symmetry assumption. A representative enterprise i is assumed to produce output Yi (say, cotton) under a decreasing returns to scale (DRS) Cobb-Douglas technology given by
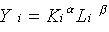 i {1,2,...,m} , > 0, + < 1 (1)
i {1,2,...,m} , > 0, + < 1 (1)
where Ki is the aggregate capital input composed of physical capital and land employed by the ith enterprise and Li is the total labor hours satisfying
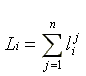 i {1,2,...,m} (2)
i {1,2,...,m} (2)
where l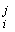 is the labor hours spent by the jth
worker/slave employed by the ith
entrepreneur/slave owner.
is the labor hours spent by the jth
worker/slave employed by the ith
entrepreneur/slave owner.
The entrepreneurs are considered to be price takers in capital and final product markets where the price for the produced good is given by P . The cost of renting one unit of aggregate capital input is given by the market rental of capital, r >0 . Total rental cost of the optimal capital stock for each enterprise will then be equal to rKi where Ki is the capital stock at which the marginal revenue from employing an additional unit of capital is equal to its marginal cost. That is,
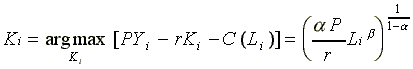 i
{1,2,...,m} . (3)
i
{1,2,...,m} . (3)
V, the value added
by labor in a system is defined as the residual income left after
paying for all costs other than wages. Letting vf
denote value added per worker in a free labor economy, it follows
from (3) that
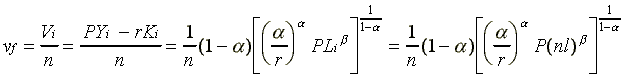
i {1,2,...,m} (4a)
implying that vf can be expressed as a function of n and l for all i.
The determination of the wage rate, w, differs across systems but the utility function of each worker or slave is assumed to be of the form:
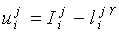
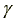 > 1, (5)
> 1, (5)
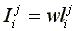 , (i,j) {1,2,...,m}{1,2,...,n} (6)
, (i,j) {1,2,...,m}{1,2,...,n} (6)
where 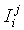 denotes the wage income of the jth
worker (slave) employed at the ith
enterprise. The
condition
denotes the wage income of the jth
worker (slave) employed at the ith
enterprise. The
condition 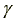 >1 is necessary in order
to assure the nonnegativity of the wage elasticity of labor supplied.
>1 is necessary in order
to assure the nonnegativity of the wage elasticity of labor supplied.
The subsistence income is
calculated by setting the utility in equation (5) equal to the
reservation level. For reservation level set equal to zero,  would represent the income that just suffices to counterbalance
the worker's disutility from work (Dirickx and Sertel, 1979),
i.e.,
would represent the income that just suffices to counterbalance
the worker's disutility from work (Dirickx and Sertel, 1979),
i.e.,
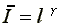 .
(7)
.
(7)
In all systems, the ratio of the equilibrium wage to the value of marginal product of labor (MPL) is given by:
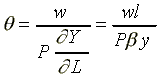 (8)
(8)
where y denotes the output per worker.
e denotes the value
added per capita after compensating the workers (slaves) for their
disutility of work, e=v-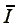 (Dirickx
and Sertel, 1979). In a society where resources are fully employed
and the number of workers is given, e can be taken as a
measure of efficiency since a higher level of e would be
necessary for a Pareto improvement.
(Dirickx
and Sertel, 1979). In a society where resources are fully employed
and the number of workers is given, e can be taken as a
measure of efficiency since a higher level of e would be
necessary for a Pareto improvement.
In cases where a free labor
market prevails, the utility maximizing choice of labor contribution
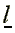 of a worker facing a given wage rate
w is
of a worker facing a given wage rate
w is
 (9)
(9)
which can be used to derive
a free worker's offer curve, i.e., the income level for which
a worker is willing to offer 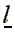 hours of
his labor:
hours of
his labor:

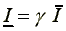 . (10)
. (10)
When n is constant, the profit maximizing choice of labor hours to be demanded from each worker by the employer for a given wage rate w, is given by
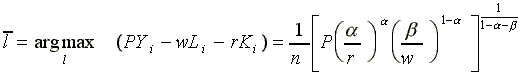 .
(11)
.
(11)
For a complete analysis,
one should also consider the offer curve of the employer, i.e.,
the maximum amount that the employer is willing to pay in order
to procure 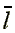 hours of labor:
hours of labor:
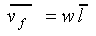
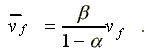 (12)
(12)
The System of Slavery
The analysis here emphasizes the quasi-capital structure of slaves. Unlike workers in other political economies, the slaves in the system of slavery are bought and sold in the market. Thus, total labor cost of an enterprise can be separated into two components: the subsistence income that should be given out to slaves, and the purchasing price of slaves themselves. Given this nature of the slavery system, a special treatment is required with respect to the assumptions of the analytical framework to be employed. In the nutshell analysis of Dirickx and Sertel (1979), for example, the systems are characterized by a fixed supply of labor. While this is a reasonable short-run assumption for other political economies, it need not be the case for slavery where slave imports may increase the supply of labor even in the short-run. Should one consider the slavery in North America, for example, slave owners created demand for the services of the slavers (slave traders) who, in turn, supplied the slave owners to the point where the formers' marginal cost equaled his marginal revenue. This implies, differently from the case of a free working population where the number of workers in the system is given to the entrepreneurs who have no significant control over the size of the total work force, that total number of slaves in slavery is a decision variable of the slave owners. So, the feasibility of slave imports makes it possible that there may be large increases in the slave population even during periods of time that would be too short to allow for a significant growth of a free working population. The following analysis accounts for this possibility by maintaining the assumption that the number of workers is fixed only for the cases where a free labor market prevails. For the case of slavery, on the other hand, the assumption is relaxed and the total number of slaves employed is determined endogenously.
Just like capital and land,
slaves are considered to have an imputed rental which represents
the opportunity cost of holding one slave instead of purchasing
an alternative asset which is taken here as the aggregate capital
good. Under perfect foresight, the absence of arbitrage requires
that satisfy:
 (13)
(13)
where t is time, P
denotes prices, denotes the constant rates of depreciation, Pt
=Pt+1-Pt,
and the superscripts S
and K
stand for slaves and the capital good, respectively. Since r
>0 and K<1,
 implying that is directly related
to current slave prices.
implying that is directly related
to current slave prices.
Ignoring supervision costs, total labor cost of the ith slave owner depends on two variables: total amount of labor and number of slaves employed. It follows naturally that the labor cost can be separated into two parts: the cost of employing n slaves and the total amount of subsistence income that should be given out to the slaves, i.e.,
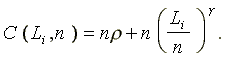 (14a)
(14a)
Therefore, the value added per capita in the system of slavery can be expressed as:
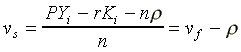 (4b)
(4b)
Assuming that the slave owners behave rationally, a slave owner who needs to employ a total of Li hours of labor would try to minimize his labor cost by adjusting n, the number of slaves. Denoting the cost minimizing level of n by
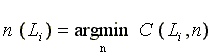
one obtains  (15)
(15)
implying that the minimum cost of labor can be expressed as a function of the total amount of labor Li employed by each slave owner alone. Then, equation (14a) would yield
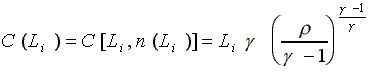 .
(14b)
.
(14b)
The number of slaves employed
is automatically adjusted to the optimal level. The profit maximizing
levels of demand for labor and the aggregate capital input by
the ith
slave owner can be found through
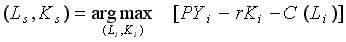 .
.
When the relevant expressions
for LS
and KS
are substituted into previous equations, one can easily derive
the expressions for n(LS),
S
and those for the per capita values of other key variables of
the system as reported in the first column of the table given
in the next section.
Since the income given out to the slaves is just enough to meet their subsistence needs, the utility of slaves turns out to be 0. An increase in the relative price of the output results in an increased demand for land, capital and slaves, leading to increased production and higher profits. In such a case, the increased demand for labor is met by increasing the number of slaves employed, as this is more cost efficient than increasing the number of labor hours supplied by each slave. The increase in the amount of capital and land employed has a positive effect on marginal productivity of labor, but this effect is offset by the increase in the number of slaves employed. Thus, the output per slave turns out to be inversely related to the output price P, whereas profits per slave is independent of P.
S, the ratio of the equilibrium subsistence wage to the value of marginal product of labor is strictly smaller than 1, and is indirectly related to the coefficient of disutility from work, . Following from the special labor cost structure in the system of slavery (where the equilibrium value of marginal product of labor is affected by both the marginal cost of subsistence compensation and marginal cost of employing one more slave), this analytical result is supported by Vedder, et. al. (1990) where S under the system of American slavery is argued to be smaller than 1/3.
An increase in slave prices
is reflected through an increase in leading, in turn, to a decline
in the overall size of the operation as reflected by declining
values of n, LS,
KS,
YS
and S.
The increase in slave prices also affects the labor cost structure,
since the slave owners tend to increase subsistence wages and
make each slave work more, instead of employing a large number
of slaves. Therefore, when slave prices go up, subsistence wages
w, labor supplied per slave l, output per capita
y, and profit per capita p tend to increase.
Free Labor Systems
This section retains the assumptions on technology and preferences but extends the foregoing discussion to free labor markets along a continuum of demand side Cournotic competition, ranging from monopsony to perfect competition in the limit.
Given L, total amount of labor employed in the system, L-i=L-Li denotes the total labor employed by all enterprises other than the ith. In a free labor market, each worker is free to choose the amount of labor he will supply. The workers determine this amount through the solution of their utility maximization problem. It follows from equation (9) that the wage rate in a free labor market with N symmetric workers will satisfy
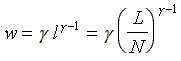 .
(16)
.
(16)
The profit function of the
ith
enterprise in an oligopsonistic free labor market can then be
expressed as
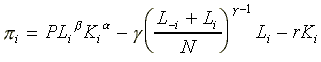 .
(17)
.
(17)
The solutions to the profit
maximization problems of the individual enterprises result in
m necessary conditions for a Cournot-Nash equilibrium in
the free labor market with m buyers:
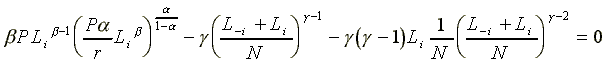 i{1,2,...,m}
. (18)
i{1,2,...,m}
. (18)
When (18) is solved for Li, i{1,2,...,m}, the equilibrium values of the key variables can be derived as reported in the Appendix. When n is constant, perfect competition equilibrium is reached in the limit as the number of firms (m) tends to infinity, and for m=1, the expressions derived would represent the equilibrium values in a monopsonistic free labor market. Finally, when the number of enterprises is finite and strictly greater than 1, oligopsony prevails in the labor market. The results indicate that total profits of an individual enterprise in a free labor market that is perfectly competitive on the supply side, i.e., f in equation (A5) of the Appendix, are directly related to the size of the total work force N, and that profits per capita is strictly decreasing in the number of enterprises, m.
The comparison of the values
of l, y, p, w and u in free
labor markets characterized by varying degrees of demand side
Cournotic competition to those under slavery is only possible
for comparable employment levels. This requires setting n
relevant to free labor systems equal to n(Lis),
the endogenously determined level of employment under slavery.
This is done by plugging the expression for n(Lis)
in equation (A3) of the Appendix into the relevant expressions
for lf , yf , pf
, wf and uf -equations
(A6) through (A10). The resulting (per capita) values for each
of these key variables are reported in the second column of the
table on the next page where the subscripts s and f
stand for the system of slavery and the free labor markets, respectively.
The third and the fourth columns of the table extend the results
to the case of a constant returns to scale (CRS) technology with
the homogeneity of the production function measured by 1- approaching
to 1. Given that the agents are taken to be symmetric, it would
suffice to consider the results for the ith
plantation alone under both technological assumptions.
Intersystematic Comparisons and Conclusions
Under the DRS technology
assumption, a comparison of free labor markets to slavery in terms
of l, y, p, w, u and would
yield the ranking in (19) below, where the superscripts C,
O and M stand for competition, oligopsony and monopsony
in the free labor
market, respectively. Given
that the level of employment was held the same at n(LS),
the endogenous level of employment solved under slavery, the ranking
in (19) could be interpreted as showing the directions the values
of key variables would take immediately following a sudden end
to slavery, depending upon the degree of demand side competition
in the emerging market for free labor. Ruling out the possibility
of migration of newly freed slaves out of the geographical region
under consideration for the moment, this degree, in turn, would
be determined by the number of slaveholding enterprises at the
time of emancipation.
Labor supplied per capita:
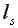 =
= 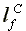 >
> 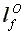 >
> 
Output per capita: 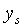 =
= 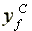 >
> 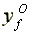 >
>
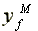
Profits per capita: 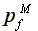 >
>
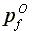 >
> 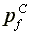 =
= 
Equilibrium wage rate:
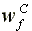 >
>
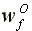 >
> 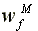 >
> 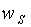 (19)
(19)
Utility level: 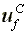 >
>
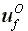 >
> 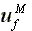 >
> 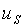
Equilibrium wage rate/MPL:
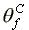 >
>  >
>
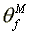 =
= 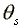
The only modification to (19)
that would be required by a change in the assumption about production
technology concerns the ranking of wages. Under the assumption
of a CRS technology, the fourth line would read:
Equilibrium wage rate:
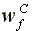 >
>
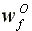 >
> 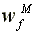 =
= 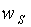
with the last inequality turned
into an equality.
S: Slavery Solution
C: Competitive Solution
M: Monopsony Solution
The figure above depicts
the offer curves of laborers and employers, and the respective
equilibria of different systems under consideration. In the figure,
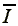 is the subsistence income necessary for
a laborer to provide l hours of his labor -equation (7),
and
is the subsistence income necessary for
a laborer to provide l hours of his labor -equation (7),
and 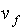 is the maximum amount that an employer
is willing to pay in order to procure l hours of labor
-equation (4a)- without allowing for negative profits to persist.
Therefore, the intersection of the areas above
is the maximum amount that an employer
is willing to pay in order to procure l hours of labor
-equation (4a)- without allowing for negative profits to persist.
Therefore, the intersection of the areas above 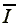 and below
and below 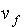 corresponds to the feasible
region of any economy. Likewise,
corresponds to the feasible
region of any economy. Likewise, 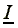 represents
the offer curve of a free worker, i.e., the income level for
which he is willing to offer l hours of his labor -equation
(10), whereas
represents
the offer curve of a free worker, i.e., the income level for
which he is willing to offer l hours of his labor -equation
(10), whereas 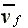 represents the offer curve
of an employer, i.e., the maximum amount that he is willing to
pay in order to procure l hours of labor -equation (12).
As expected, the intersection point of the two offer curves, C,
corresponds to the competitive equilibrium, where both the employers
and the laborers behave as price takers. The free labor market
solutions lie on
represents the offer curve
of an employer, i.e., the maximum amount that he is willing to
pay in order to procure l hours of labor -equation (12).
As expected, the intersection point of the two offer curves, C,
corresponds to the competitive equilibrium, where both the employers
and the laborers behave as price takers. The free labor market
solutions lie on 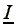 between points M
and C. Under slavery, the relevant offer curve of the
slave owner-entrepreneur (planter) would be
between points M
and C. Under slavery, the relevant offer curve of the
slave owner-entrepreneur (planter) would be 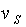 in
equation (4b), and would deviate from
in
equation (4b), and would deviate from 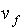 by .
by .
It can easily be checked
for given values of and n=n(Lis)
that 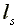 =
=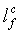 maximizes
es
and ef
. Technically speaking, this implies that the slavery and perfect
competition in the labor market operate at socially efficient
levels, whereas the monopsony and oligopsony in the labor market
are inefficient. At first sight, this assertion may seem to contradict
the inequalities
maximizes
es
and ef
. Technically speaking, this implies that the slavery and perfect
competition in the labor market operate at socially efficient
levels, whereas the monopsony and oligopsony in the labor market
are inefficient. At first sight, this assertion may seem to contradict
the inequalities 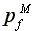 >
>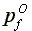 >
>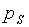 and
and  >
> >
>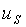 in (19) for they imply together that both slave owners and
slaves are worse off in the 'efficient' system of slavery, compared
to the inefficient systems of monopsony and oligopsony in the
labor market. The explanation for this apparent contradiction
can be found through a careful examination of the figure which
suggests that, in the system of slavery, the slave owners' surplus
is not only
in (19) for they imply together that both slave owners and
slaves are worse off in the 'efficient' system of slavery, compared
to the inefficient systems of monopsony and oligopsony in the
labor market. The explanation for this apparent contradiction
can be found through a careful examination of the figure which
suggests that, in the system of slavery, the slave owners' surplus
is not only 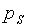 but
but 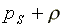 .
This is a natural implication of the set of property rights in
the system of slavery which entitle the slave owners to the (imputed)
rental of their quasi-capital holdings, slaves.
.
This is a natural implication of the set of property rights in
the system of slavery which entitle the slave owners to the (imputed)
rental of their quasi-capital holdings, slaves.
Turning back to the static
comparisons in expression (19), a good question to ask concerns
the reason why the slave owners did not abolish slavery, even
though they had a chance to improve their profits in the short
run by adopting a free labor market. The answer to this question
is twofold. Firstly, in the system of slavery, the surplus of
slave owners is not made up of only the operational profits but
also includes the (imputed) rental of the slaves already owned.
Thus, the abolishment of slavery would impose a burden on the
slave owners amounting to per slave per period. Note that for
all free labor economies under consideration 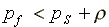 ,
implying that the profits alone would not account for total gains
of the slave owners from the maintenance of slavery. In other
words, the slave owners would be made worse off by a transition
to a free labor economy despite the inequality
,
implying that the profits alone would not account for total gains
of the slave owners from the maintenance of slavery. In other
words, the slave owners would be made worse off by a transition
to a free labor economy despite the inequality 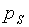 <
<
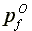 <
< . The second
reason is the risk of ending up with a smaller labor force and
hence, lower profits after the abolishment of slavery, due to
the migration of freed slaves to other parts of the country (Mandle,
1992; Graves, et.al., 1983).
. The second
reason is the risk of ending up with a smaller labor force and
hence, lower profits after the abolishment of slavery, due to
the migration of freed slaves to other parts of the country (Mandle,
1992; Graves, et.al., 1983).
The degree of demand side competition in the free labor market of a system alternative to slavery depends on the number of planters. Remembering that pf is strictly decreasing in m, the change in the profits per capita after the abolishment of slavery is inversely related to the number of plantations. Along with the negative effects of emancipation on the slave owners mentioned in the previous paragraph, this would imply a stronger resistance against slavery in the regions having a large number of small planters, compared to those regions with few large planters. Similarly, on an intertemporal basis, a ceteris paribus decline (increase) in the number of planters in a region would be likely to reduce (increase) resistance against the abolishment of slavery.
The ranking in (19) also
indicates that , the value of the equilibrium wage to the value
of marginal product of labor, attains its lower bound (the inverse
of the coefficient of disutility from work, 1/) in the case of
slavery and monopsony in the labor market. The upper bound for
is 1 and this value is reached only at the limit as m
tends to infinity, i.e., under perfect competition in the labor
market. When the demand side competition in the labor market is
characterized by oligopsony, will strictly increase in m
and take a value that lies strictly between its lower and upper
bounds. This ranking of possible values for implies that the
labor will be paid the value of its marginal product only when
there is a large number of enterprises competing to attract workers,
and the ratio of labor earnings to MPL will decline as m
falls. It is worth noting that the existence of a single buyer
in the labor market, i.e., monopsony, is not different than slavery
when compared in terms of this ratio.
Appendix
 (A1)
(A1)
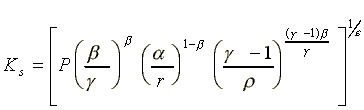 (A2)
(A2)
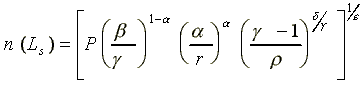 (A3)
(A3)
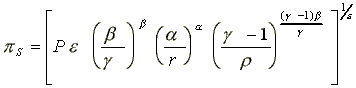 (A4)
(A4)
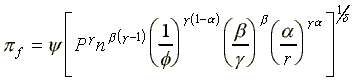 (A5)
(A5)
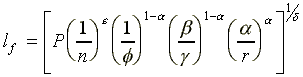 (A6)
(A6)
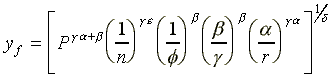 (A7)
(A7)
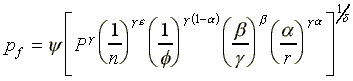 (A8)
(A8)
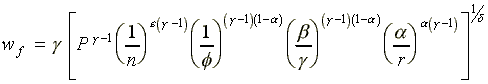 (A9)
(A9)
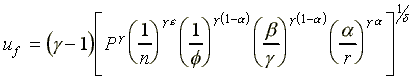 (A10)
(A10)
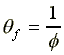 (A11)
(A11)
where =1--, =(1-)- , =1+(-1)/m, =(1-)- and the subscripts s and f stand for the system of slavery and the oligopsonistic free labor market, respectively.
References
Chwe, Michael Suk Young (1990).
Why were Workers Whipped? Pain in a Principal-Agent Model. Economic
Journal, 100 (403): 1109-21.
David, Paul A. and Temin,
Peter (1979). Explaining the Relative Efficiency of Slave Agriculture
in the Antebellum South: A Comment. American Economic Review,
69 (1): 211-12.
de Dios, Emmanuel S. (1990).
Preliminary Notes on Modes of Production. Philippine Review
of Economics and Business, 27 (1): 8-18.
Dirickx, Yvo M.I. and Sertel,
Murat R. (1979). The Comparative Political Economy of Workers'
Management and Capitalism in a Nutshell. European Institute for
Advanced Studies in Management Working Paper No. 79-2.
Dirickx, Yvo M.I. and Sertel,
Murat R. (1978). Comparative Political Economy of Capitalism,
Communism, Slavery and Colonialism in a Nutshell. Recherches
Economiques de Louvain, 44, no. 3.
Fenoaltea, Stefano (1984).
Slavery and Supervision in Comparative Perspective: A Model. Journal
of Economic History, 44 (3): 635-68.
Field, Elisabeth B. (1988).
The Relative Efficiency of Slavery Revisited: A Translog Production
Function Approach. American Economic Review, 78 (3): 543-49.
Findlay, Ronald (1975). Slavery,
Incentives and Manumission: A Theoretical Model. Journal of
Political Economy, 83 (5): 923-33.
Fleisig, Heywood (1976).
Slavery, the Supply of Agricultural Labor, and the Industrialization
of the South. Journal of Economic History, 34 (3): 572-97.
Fogel, Robert W. (1989).
Without Consent or Contract: The Rise and Fall of American
Slavery. New York: W.W. Norton.
Fogel, Robert W. and Engerman,
Stanley L. (1980). Explaining the Relative Efficiency of Slave
Agriculture in the Antebellum South: Reply. American Economic
Review, 70 (4): 672-90.
Fogel, Robert W. and Engerman,
Stanley L. (1977). Explaining the Relative Efficiency of Slave
Agriculture in the Antebellum South. American Economic Review,
67 (3): 275-96.
Fogel, Robert W. and Engerman,
Stanley L. (1974). Time on the Cross: The Economics of American
Negro Slavery. Boston: Little Brown.
Fogel, Robert W. and Engerman,
Stanley L. (eds.) (1971). The Reinterpretation of American
Economic History . New York: Harper & Row.
Graves, Philip E., Sexton,
Robert L. and Vedder, Richard K. (1983). Slavery, Amenities, and
Factor Price Equalization: A Note on Migration and Freedom. Explorations
in Economic History, 20: 156-62.
Haskell, Thomas L. (1979).
Explaining the Relative Efficiency of Slave Agriculture in the
Antebellum South: A Reply to Fogel-Engerman. American Economic
Review, 69 (1): 206-7.
Mandle, Jay R. (1992). Not
Slave not Free: The African American Economic Experience since
the Civil War. Durham and London: Duke University Press.
Ransom, Roger L. and Sutch,
Richard (1988). Capitalists without Capital: The Burden of Slavery
and the Impact of Emancipation. University of California at Berkeley
Working Paper in Economics: 8867, February, 54.
Schaefer, Donald F. and Schmitz,
Mark D. (1979). The Relative Efficiency of Slave Agriculture:
A Comment. American Economic Review, 69 (1): 208-12.
Vedder, Richard K., Gallaway,
L. and Klingaman, D. C. (1990). Black Exploitation and White
Benefits: The Civil War Income Revolution. In R. America (ed.),
The Wealth of Races: The Present Value of Benefits from Past
Injustices. Westport and London: Greenwood.
Wright, Gavin (1997). Slavery
and Commerce in the Colonial Era. Lecture Notes. Stanford University.
Wright, Gavin (1991). What
was Slavery? Social Concept, 6: 29-51.
Wright, Gavin (1979). The
Efficiency of Slavery: Another Interpretation. American Economic
Review, 69 (1): 219-26.
Wright, Gavin (1976). Prosperity,
Progress and American Slavery. In Paul A. David et.al.
(eds.), Reckoning with Slavery. New York.